| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Example 1 to 5 (Before Exercise 7.1) | Exercise 7.1 | Example 6 to 10 (Before Exercise 7.2) |
| Exercise 7.2 | Example 11 to 15 (Before Exercise 7.3) | Exercise 7.3 |
| Exercise 7.4 (Optional) | ||
Chapter 7 Coordinate Geometry
Welcome to the solutions for Chapter 7: Coordinate Geometry. This chapter marks a significant development in our study of geometry by introducing powerful algebraic techniques to analyze geometric figures and relationships within the Cartesian coordinate plane. Building upon foundational concepts learned in Class 9, such as plotting points and understanding coordinates, this chapter equips us with specific formulas that allow us to calculate distances, find coordinates of points dividing segments in specific ratios, and determine areas of polygons using only the coordinates of their vertices. Coordinate geometry, pioneered by René Descartes, provides a remarkable bridge between the visual world of geometry and the symbolic manipulation of algebra, enabling us to solve geometric problems with algebraic precision and vice versa. It transforms points into ordered pairs $(x, y)$, lines into equations, and geometric properties into algebraic conditions.
The first fundamental tool introduced is the Distance Formula. Derived directly from the Pythagorean theorem, this formula provides the straight-line distance $d$ between any two points $A(x_1, y_1)$ and $B(x_2, y_2)$ in the plane. The formula is given by:
$d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$
The solutions meticulously demonstrate the diverse applications of this formula. Beyond simply finding the length of a line segment, it is instrumental in:
- Calculating the side lengths of various polygons (triangles, quadrilaterals).
- Checking for collinearity of three or more points (if points A, B, C are collinear, the sum of the lengths of two segments, e.g., $AB + BC$, will equal the length of the third segment, $AC$).
- Identifying the type of triangle formed by three points (scalene, isosceles, equilateral, right-angled) by comparing side lengths.
- Classifying quadrilaterals (as parallelograms, rectangles, squares, or rhombuses) by examining the lengths of sides and diagonals.
The second major instrument explored is the Section Formula. This formula determines the coordinates $P(x, y)$ of a point that divides the line segment joining two given points, $A(x_1, y_1)$ and $B(x_2, y_2)$, internally in a specified ratio $m_1 : m_2$. The coordinates are calculated as:
$x = \frac{m_1x_2 + m_2x_1}{m_1 + m_2}, \quad y = \frac{m_1y_2 + m_2y_1}{m_1 + m_2}$
Solutions showcase its utility in various scenarios, including finding points of trisection (where a segment is divided into three equal parts, requiring ratios $1:2$ and $2:1$), deriving the coordinates of the mid-point of a segment (a special case where $m_1 = m_2 = 1$, simplifying the formula to the Mid-point Formula: $x = \frac{x_1+x_2}{2}$, $y = \frac{y_1+y_2}{2}$), and determining the ratio in which a given point (or the x-axis/y-axis) divides a line segment.
The third key formula presented enables the calculation of the Area of a Triangle directly from the coordinates of its vertices, $(x_1, y_1)$, $(x_2, y_2)$, and $(x_3, y_3)$. The formula is:
$Area = \frac{1}{2} |x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)|$
The absolute value ensures the area is positive. Solutions demonstrate its use not only for calculating the area of triangles but also as another method to check for the collinearity of three points – if the area calculated using this formula is zero, the points lie on the same straight line. These three formulas collectively provide a robust toolkit for analytical geometry, merging algebraic computation with geometric insight.
Example 1 to 5 (Before Exercise 7.1)
Example 1. Do the points (3, 2), (–2, –3) and (2, 3) form a triangle? If so, name the type of triangle formed.
Answer:
Given:
Let the given points be $A = (3, 2)$, $B = (–2, –3)$ and $C = (2, 3)$.
To Find:
To determine if the points A, B, and C form a triangle. If yes, to name the type of triangle formed.
Solution:
We use the distance formula to find the lengths of the segments joining these points.
The distance between two points $(x_1, y_1)$ and $(x_2, y_2)$ is given by:
$d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$
Calculating the length of segment AB:
$AB = \sqrt{(-2 - 3)^2 + (-3 - 2)^2}$
$AB = \sqrt{(-5)^2 + (-5)^2}$
$AB = \sqrt{25 + 25}$
$AB = \sqrt{50} = 5\sqrt{2}$ units.
Calculating the length of segment BC:
$BC = \sqrt{(2 - (-2))^2 + (3 - (-3))^2}$
$BC = \sqrt{(2 + 2)^2 + (3 + 3)^2}$
$BC = \sqrt{(4)^2 + (6)^2}$
$BC = \sqrt{16 + 36}$
$BC = \sqrt{52} = 2\sqrt{13}$ units.
Calculating the length of segment AC:
$AC = \sqrt{(2 - 3)^2 + (3 - 2)^2}$
$AC = \sqrt{(-1)^2 + (1)^2}$
$AC = \sqrt{1 + 1}$
$AC = \sqrt{2}$ units.
For the points to form a triangle, the sum of the lengths of any two sides must be greater than the length of the third side (Triangle Inequality Theorem).
Check 1: $AB + AC > BC$?
$5\sqrt{2} + \sqrt{2} = 6\sqrt{2} = \sqrt{72}$.
$BC = \sqrt{52}$.
Since $72 > 52$, $\sqrt{72} > \sqrt{52}$. Thus, $AB + AC > BC$.
Check 2: $AB + BC > AC$?
$5\sqrt{2} + 2\sqrt{13} = \sqrt{50} + \sqrt{52}$.
$AC = \sqrt{2}$.
Since $\sqrt{50} > \sqrt{2}$ and $\sqrt{52} > 0$, clearly $\sqrt{50} + \sqrt{52} > \sqrt{2}$. Thus, $AB + BC > AC$.
Check 3: $BC + AC > AB$?
$2\sqrt{13} + \sqrt{2} = \sqrt{52} + \sqrt{2}$.
$AB = \sqrt{50}$.
Since $\sqrt{52} > \sqrt{50}$ and $\sqrt{2} > 0$, clearly $\sqrt{52} + \sqrt{2} > \sqrt{50}$. Thus, $BC + AC > AB$.
Since all three triangle inequalities hold true, the points A, B, and C do form a triangle.
Type of Triangle:
To determine the type of triangle, we examine the side lengths and check for properties like equal sides or right angles.
The side lengths are $AB = \sqrt{50}$, $BC = \sqrt{52}$, and $AC = \sqrt{2}$.
Since all three side lengths are different, the triangle is a scalene triangle.
Now, let's check if it's a right-angled triangle using the converse of the Pythagorean theorem. We compare the square of the longest side with the sum of the squares of the other two sides.
The squares of the side lengths are:
$AB^2 = (\sqrt{50})^2 = 50$
$BC^2 = (\sqrt{52})^2 = 52$
$AC^2 = (\sqrt{2})^2 = 2$
The longest side is $BC$. We check if $BC^2 = AB^2 + AC^2$.
$AB^2 + AC^2 = 50 + 2 = 52$
$BC^2 = 52$
Since $BC^2 = AB^2 + AC^2$, the triangle satisfies the condition for a right-angled triangle (converse of Pythagoras' theorem), with the right angle opposite the longest side BC, i.e., at vertex A.
Therefore, the triangle formed by the points (3, 2), (–2, –3) and (2, 3) is a right-angled triangle.
Example 2. Show that the points (1, 7), (4, 2), (–1, –1) and (– 4, 4) are the vertices of a square
Answer:
Given:
Let the given points be $A = (1, 7)$, $B = (4, 2)$, $C = (-1, -1)$, and $D = (-4, 4)$.
To Prove:
The points A, B, C, and D are the vertices of a square.
Proof:
To show that the given points form a square, we need to demonstrate two properties:
1. All four sides of the quadrilateral formed by these points are equal in length.
2. The lengths of the two diagonals are equal.
We will use the distance formula to find the lengths of the sides and diagonals. The distance between two points $(x_1, y_1)$ and $(x_2, y_2)$ is given by:
$d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$
Calculating the lengths of the four sides:
Length of side AB:
$AB = \sqrt{(4 - 1)^2 + (2 - 7)^2}$
$AB = \sqrt{(3)^2 + (-5)^2}$
$AB = \sqrt{9 + 25} = \sqrt{34}$ units.
Length of side BC:
$BC = \sqrt{(-1 - 4)^2 + (-1 - 2)^2}$
$BC = \sqrt{(-5)^2 + (-3)^2}$
$BC = \sqrt{25 + 9} = \sqrt{34}$ units.
Length of side CD:
$CD = \sqrt{(-4 - (-1))^2 + (4 - (-1))^2}$
$CD = \sqrt{(-4 + 1)^2 + (4 + 1)^2}$
$CD = \sqrt{(-3)^2 + (5)^2}$
$CD = \sqrt{9 + 25} = \sqrt{34}$ units.
Length of side DA:
$DA = \sqrt{(1 - (-4))^2 + (7 - 4)^2}$
$DA = \sqrt{(1 + 4)^2 + (3)^2}$
$DA = \sqrt{(5)^2 + (3)^2}$
$DA = \sqrt{25 + 9} = \sqrt{34}$ units.
Since $AB = BC = CD = DA = \sqrt{34}$, all four sides of the quadrilateral ABCD are equal. This confirms that ABCD is at least a rhombus.
Calculating the lengths of the two diagonals:
Length of diagonal AC:
$AC = \sqrt{(-1 - 1)^2 + (-1 - 7)^2}$
$AC = \sqrt{(-2)^2 + (-8)^2}$
$AC = \sqrt{4 + 64} = \sqrt{68}$ units.
Length of diagonal BD:
$BD = \sqrt{(-4 - 4)^2 + (4 - 2)^2}$
$BD = \sqrt{(-8)^2 + (2)^2}$
$BD = \sqrt{64 + 4} = \sqrt{68}$ units.
Since $AC = BD = \sqrt{68}$, the lengths of the two diagonals are equal.
Because all four sides are equal ($AB=BC=CD=DA$) and the two diagonals are equal ($AC=BD$), the quadrilateral formed by the points A, B, C, and D satisfies the properties of a square.
Therefore, the points (1, 7), (4, 2), (–1, –1) and (– 4, 4) are the vertices of a square.
Example 3. Fig. 7.6 shows the arrangement of desks in a classroom. Ashima, Bharti and Camella are seated at A(3, 1), B(6, 4) and C(8, 6) respectively. Do you think they are seated in a line? Give reasons for your answer.
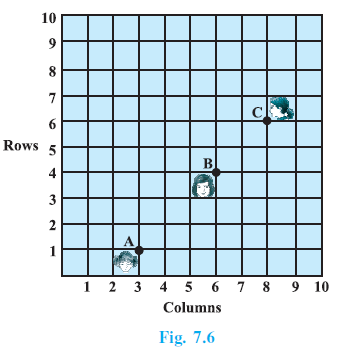
Answer:
Given:
The positions of Ashima, Bharti, and Camella are represented by the points A(3, 1), B(6, 4), and C(8, 6) respectively.
To Find:
To determine if the points A, B, and C lie on the same straight line.
Solution:
Three points are collinear if the sum of the lengths of any two line segments formed by these points is equal to the length of the remaining line segment.
We will use the distance formula to find the lengths of the segments AB, BC, and AC. The distance between two points $(x_1, y_1)$ and $(x_2, y_2)$ is given by:
$d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$
Calculating the length of segment AB:
$AB = \sqrt{(6 - 3)^2 + (4 - 1)^2}$
$AB = \sqrt{(3)^2 + (3)^2}$
$AB = \sqrt{9 + 9}$
$AB = \sqrt{18} = 3\sqrt{2}$ units.
Calculating the length of segment BC:
$BC = \sqrt{(8 - 6)^2 + (6 - 4)^2}$
$BC = \sqrt{(2)^2 + (2)^2}$
$BC = \sqrt{4 + 4}$
$BC = \sqrt{8} = 2\sqrt{2}$ units.
Calculating the length of segment AC:
$AC = \sqrt{(8 - 3)^2 + (6 - 1)^2}$
$AC = \sqrt{(5)^2 + (5)^2}$
$AC = \sqrt{25 + 25}$
$AC = \sqrt{50} = 5\sqrt{2}$ units.
Now, we check if the sum of the lengths of the two smaller segments equals the length of the longest segment.
Check if $AB + BC = AC$.
$AB + BC = 3\sqrt{2} + 2\sqrt{2} = (3+2)\sqrt{2} = 5\sqrt{2}$ units.
We found that $AC = 5\sqrt{2}$ units.
Since $AB + BC = AC$ ($3\sqrt{2} + 2\sqrt{2} = 5\sqrt{2}$), the points A, B, and C are collinear.
Therefore, Yes, Ashima, Bharti, and Camella are seated in a line.
Example 4. Find a relation between x and y such that the point (x , y) is equidistant from the points (7, 1) and (3, 5).
Answer:
Given:
Let $P(x, y)$ be a point that is equidistant from the points $A(7, 1)$ and $B(3, 5)$.
To Find:
A relation between $x$ and $y$.
Solution:
Since point $P(x, y)$ is equidistant from points $A(7, 1)$ and $B(3, 5)$, the distance $PA$ must be equal to the distance $PB$.
We use the distance formula: The distance between two points $(x_1, y_1)$ and $(x_2, y_2)$ is $\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$.
Calculating the distance PA:
$PA = \sqrt{(7 - x)^2 + (1 - y)^2}$
Calculating the distance PB:
$PB = \sqrt{(3 - x)^2 + (5 - y)^2}$
According to the given condition, $PA = PB$.
$\sqrt{(7 - x)^2 + (1 - y)^2} = \sqrt{(3 - x)^2 + (5 - y)^2}$
Squaring both sides to eliminate the square roots:
$(7 - x)^2 + (1 - y)^2 = (3 - x)^2 + (5 - y)^2$
Expanding the terms:
$(49 - 14x + x^2) + (1 - 2y + y^2) = (9 - 6x + x^2) + (25 - 10y + y^2)$
Combine like terms on each side:
$x^2 - 14x + y^2 - 2y + 50 = x^2 - 6x + y^2 - 10y + 34$
Subtract $x^2$ and $y^2$ from both sides:
$-14x - 2y + 50 = -6x - 10y + 34$
Rearrange the terms to bring variables to one side and constants to the other:
$-14x + 6x - 2y + 10y = 34 - 50$
Combine like terms:
$-8x + 8y = -16$
Divide the entire equation by -8:
$\frac{-8x}{-8} + \frac{8y}{-8} = \frac{-16}{-8}$
$x - y = 2$
This is the required relation between $x$ and $y$.
Therefore, the relation is $x - y = 2$.
Example 5. Find a point on the y-axis which is equidistant from the points A(6,5) and B(– 4, 3).
Answer:
Given:
Two points $A(6, 5)$ and $B(-4, 3)$.
We need to find a point on the y-axis which is equidistant from A and B.
To Find:
The coordinates of the point on the y-axis equidistant from A and B.
Solution:
Let the point on the y-axis be $P(0, y)$. Since any point on the y-axis has its x-coordinate as 0.
We are given that the point P is equidistant from points A and B. Therefore, $PA = PB$.
Using the distance formula, the distance between two points $(x_1, y_1)$ and $(x_2, y_2)$ is $\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$.
Calculating the distance PA:
$PA = \sqrt{(6 - 0)^2 + (5 - y)^2}$
$PA = \sqrt{(6)^2 + (5 - y)^2}$
$PA = \sqrt{36 + (5 - y)^2}$
Calculating the distance PB:
$PB = \sqrt{(-4 - 0)^2 + (3 - y)^2}$
$PB = \sqrt{(-4)^2 + (3 - y)^2}$
$PB = \sqrt{16 + (3 - y)^2}$
Since $PA = PB$, we have $PA^2 = PB^2$.
$\left(\sqrt{36 + (5 - y)^2}\right)^2 = \left(\sqrt{16 + (3 - y)^2}\right)^2$
$36 + (5 - y)^2 = 16 + (3 - y)^2$
Expanding the squared terms:
$36 + (25 - 10y + y^2) = 16 + (9 - 6y + y^2)$
$36 + 25 - 10y + y^2 = 16 + 9 - 6y + y^2$
$61 - 10y + y^2 = 25 - 6y + y^2$
Subtract $y^2$ from both sides:
$61 - 10y = 25 - 6y$
Rearrange the terms to solve for $y$:
$61 - 25 = -6y + 10y$
$36 = 4y$
$y = \frac{36}{4}$
$y = 9$
So, the coordinates of the point P on the y-axis are $(0, y) = (0, 9)$.
Therefore, the required point on the y-axis is (0, 9).
Exercise 7.1
Question 1. Find the distance between the following pairs of points :
(i) (2, 3), (4, 1)
(ii) (– 5, 7), (– 1, 3)
(iii) (a, b), (– a, – b)
Answer:
The distance between two points $(x_1, y_1)$ and $(x_2, y_2)$ is given by the distance formula:
$d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$
(i)
Given points: $(x_1, y_1) = (2, 3)$ and $(x_2, y_2) = (4, 1)$.
Using the distance formula:
$d = \sqrt{(4 - 2)^2 + (1 - 3)^2}$
$d = \sqrt{(2)^2 + (-2)^2}$
$d = \sqrt{4 + 4}$
$d = \sqrt{8}$
$d = 2\sqrt{2}$ units.
The distance between the points (2, 3) and (4, 1) is $2\sqrt{2}$ units.
(ii)
Given points: $(x_1, y_1) = (-5, 7)$ and $(x_2, y_2) = (-1, 3)$.
Using the distance formula:
$d = \sqrt{(-1 - (-5))^2 + (3 - 7)^2}$
$d = \sqrt{(-1 + 5)^2 + (-4)^2}$
$d = \sqrt{(4)^2 + (-4)^2}$
$d = \sqrt{16 + 16}$
$d = \sqrt{32}$
$d = 4\sqrt{2}$ units.
The distance between the points (–5, 7) and (–1, 3) is $4\sqrt{2}$ units.
(iii)
Given points: $(x_1, y_1) = (a, b)$ and $(x_2, y_2) = (-a, -b)$.
Using the distance formula:
$d = \sqrt{(-a - a)^2 + (-b - b)^2}$
$d = \sqrt{(-2a)^2 + (-2b)^2}$
$d = \sqrt{4a^2 + 4b^2}$
$d = \sqrt{4(a^2 + b^2)}$
$d = 2\sqrt{a^2 + b^2}$ units.
The distance between the points (a, b) and (–a, –b) is $2\sqrt{a^2 + b^2}$ units.
Question 2. Find the distance between the points (0, 0) and (36, 15). Can you now find the distance between the two towns A and B discussed in Section 7.2.
Towns provided in Section 7.2 - A town B is located 36 km east and 15 km north of the town A. How would you find the distance from town A to town B without actually measuring it.
Answer:
Part 1: Distance between points (0, 0) and (36, 15)
Let the points be $P(0, 0)$ and $Q(36, 15)$.
We use the distance formula: $d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$.
Here, $(x_1, y_1) = (0, 0)$ and $(x_2, y_2) = (36, 15)$.
Substituting the coordinates:
$d = \sqrt{(36 - 0)^2 + (15 - 0)^2}$
$d = \sqrt{(36)^2 + (15)^2}$
$d = \sqrt{1296 + 225}$
$d = \sqrt{1521}$
To find the square root of 1521:
We know $30^2 = 900$ and $40^2 = 1600$. The number ends in 1, so the square root must end in 1 or 9. Let's try 39.
$39 \times 39 = 1521$.
$d = 39$ units.
So, the distance between the points (0, 0) and (36, 15) is 39 units.
Part 2: Distance between Town A and Town B
Yes, we can find the distance between the two towns A and B using the distance formula calculated above.
Let Town A be located at the origin (0, 0) on a coordinate plane.
Since Town B is located 36 km east and 15 km north of Town A, the coordinates of Town B can be represented as (36, 15).
The distance between Town A (0, 0) and Town B (36, 15) is the same as the distance calculated in Part 1.
Distance $AB = \sqrt{(36 - 0)^2 + (15 - 0)^2}$
Distance $AB = \sqrt{36^2 + 15^2}$
Distance $AB = \sqrt{1296 + 225}$
Distance $AB = \sqrt{1521}$
Distance $AB = 39$ km.
Therefore, the distance between Town A and Town B is 39 km.
Question 3. Determine if the points (1, 5), (2, 3) and (– 2, – 11) are collinear.
Answer:
Given:
Let the points be $A = (1, 5)$, $B = (2, 3)$, and $C = (– 2, – 11)$.
To Find:
To determine if the points A, B, and C are collinear.
Solution:
Three points are collinear if they lie on the same straight line. This condition can be checked using the distance formula: if the sum of the lengths of any two line segments connecting the points is equal to the length of the third line segment, then the points are collinear.
We calculate the distances between each pair of points using the distance formula $d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$.
Calculating the distance AB:
$AB = \sqrt{(2 - 1)^2 + (3 - 5)^2}$
$AB = \sqrt{(1)^2 + (-2)^2}$
$AB = \sqrt{1 + 4}$
$AB = \sqrt{5}$ units.
Calculating the distance BC:
$BC = \sqrt{(-2 - 2)^2 + (-11 - 3)^2}$
$BC = \sqrt{(-4)^2 + (-14)^2}$
$BC = \sqrt{16 + 196}$
$BC = \sqrt{212}$ units.
Calculating the distance AC:
$AC = \sqrt{(-2 - 1)^2 + (-11 - 5)^2}$
$AC = \sqrt{(-3)^2 + (-16)^2}$
$AC = \sqrt{9 + 256}$
$AC = \sqrt{265}$ units.
Now, we check if the sum of any two distances equals the third distance.
Check if $AB + BC = AC$.
$AB + BC = \sqrt{5} + \sqrt{212}$
$AC = \sqrt{265}$
Since $\sqrt{5} + \sqrt{212} \neq \sqrt{265}$, the condition $AB + BC = AC$ is not satisfied.
We can also check the other combinations, but it's clear that the sum of the two smaller distances ($\sqrt{5}$ and $\sqrt{212}$) does not equal the largest distance ($\sqrt{265}$).
Since the sum of the lengths of any two line segments is not equal to the length of the third segment, the points A, B, and C do not lie on the same line.
Therefore, the points (1, 5), (2, 3) and (– 2, – 11) are not collinear.
Question 4. Check whether (5, – 2), (6, 4) and (7, – 2) are the vertices of an isosceles triangle.
Answer:
Given:
Let the points be $A = (5, -2)$, $B = (6, 4)$, and $C = (7, -2)$.
To Check:
Whether the points A, B, and C are the vertices of an isosceles triangle.
Solution:
An isosceles triangle is a triangle that has at least two sides of equal length. We will calculate the lengths of the sides AB, BC, and AC using the distance formula: $d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$.
Calculating the length of side AB:
$AB = \sqrt{(6 - 5)^2 + (4 - (-2))^2}$
$AB = \sqrt{(1)^2 + (4 + 2)^2}$
$AB = \sqrt{1^2 + 6^2}$
$AB = \sqrt{1 + 36}$
$AB = \sqrt{37}$ units.
Calculating the length of side BC:
$BC = \sqrt{(7 - 6)^2 + (-2 - 4)^2}$
$BC = \sqrt{(1)^2 + (-6)^2}$
$BC = \sqrt{1 + 36}$
$BC = \sqrt{37}$ units.
Calculating the length of side AC:
$AC = \sqrt{(7 - 5)^2 + (-2 - (-2))^2}$
$AC = \sqrt{(2)^2 + (-2 + 2)^2}$
$AC = \sqrt{2^2 + 0^2}$
$AC = \sqrt{4 + 0}$
$AC = \sqrt{4} = 2$ units.
Comparing the lengths of the sides:
$AB = \sqrt{37}$
$BC = \sqrt{37}$
$AC = 2$
Since $AB = BC = \sqrt{37}$, two sides of the triangle formed by points A, B, and C are equal in length.
Therefore, the points (5, – 2), (6, 4) and (7, – 2) are the vertices of an isosceles triangle.
Question 5. In a classroom, 4 friends are seated at the points A, B, C and D as shown in Fig. 7.8. Champa and Chameli walk into the class and after observing for a few minutes Champa asks Chameli, “Don’t you think ABCD is a square?” Chameli disagrees. Using distance formula, find which of them is correct.
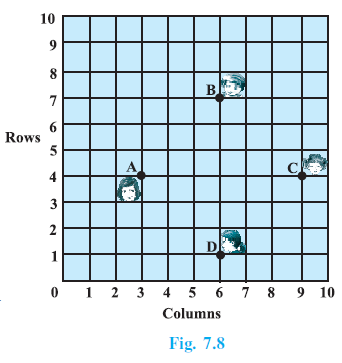
Answer:
Given:
From the figure (Fig. 7.8), the coordinates of the four friends are:
$A = (3, 4)$
$B = (6, 7)$
$C = (9, 4)$
$D = (6, 1)$
Champa believes ABCD is a square, while Chameli disagrees.
To Find:
Using the distance formula, determine if ABCD is a square and state whether Champa or Chameli is correct.
Solution:
To check if ABCD is a square, we need to calculate the lengths of all four sides (AB, BC, CD, DA) and the lengths of the two diagonals (AC, BD).
A quadrilateral is a square if:
1. All four sides are equal in length.
2. The two diagonals are equal in length.
We use the distance formula: $d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$.
Calculating the lengths of the sides:
Length of AB:
$AB = \sqrt{(6 - 3)^2 + (7 - 4)^2} = \sqrt{3^2 + 3^2} = \sqrt{9 + 9} = \sqrt{18} = 3\sqrt{2}$ units.
Length of BC:
$BC = \sqrt{(9 - 6)^2 + (4 - 7)^2} = \sqrt{3^2 + (-3)^2} = \sqrt{9 + 9} = \sqrt{18} \ $$ = 3\sqrt{2}$ units.
Length of CD:
$CD = \sqrt{(6 - 9)^2 + (1 - 4)^2} = \sqrt{(-3)^2 + (-3)^2} = \sqrt{9 + 9} = \sqrt{18} \ $$ = 3\sqrt{2}$ units.
Length of DA:
$DA = \sqrt{(3 - 6)^2 + (4 - 1)^2} = \sqrt{(-3)^2 + 3^2} = \sqrt{9 + 9} = \sqrt{18} \ $$ = 3\sqrt{2}$ units.
Since $AB = BC = CD = DA = 3\sqrt{2}$, all four sides are equal.
Calculating the lengths of the diagonals:
Length of AC:
$AC = \sqrt{(9 - 3)^2 + (4 - 4)^2} = \sqrt{6^2 + 0^2} = \sqrt{36 + 0} = \sqrt{36} = 6$ units.
Length of BD:
$BD = \sqrt{(6 - 6)^2 + (1 - 7)^2} = \sqrt{0^2 + (-6)^2} = \sqrt{0 + 36} = \sqrt{36} = 6$ units.
Since $AC = BD = 6$, the two diagonals are equal.
Because all four sides are equal ($AB = BC = CD = DA = 3\sqrt{2}$) and both diagonals are equal ($AC = BD = 6$), the quadrilateral ABCD is a square.
Therefore, Champa's observation that ABCD is a square is correct.
Conclusion: Champa is correct.
Question 6. Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer:
(i) (– 1, – 2), (1, 0), (– 1, 2), (– 3, 0)
(ii) (–3, 5), (3, 1), (0, 3), (–1, – 4)
(iii) (4, 5), (7, 6), (4, 3), (1, 2)
Answer:
(i) (– 1, – 2), (1, 0), (– 1, 2), (– 3, 0)
Solution
Let the given points be A(–1, –2), B(1, 0), C(–1, 2), and D(–3, 0).
To determine the type of quadrilateral, we will find the lengths of all four sides and both diagonals using the distance formula.
The distance between two points $(x_1, y_1)$ and $(x_2, y_2)$ is given by:
$d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$
Length of the sides:
$AB = \sqrt{(1 - (-1))^2 + (0 - (-2))^2} = \sqrt{(2)^2 + (2)^2} = \sqrt{4 + 4} \ $$ = \sqrt{8} = 2\sqrt{2}$ units.
$BC = \sqrt{(-1 - 1)^2 + (2 - 0)^2} = \sqrt{(-2)^2 + (2)^2} = \sqrt{4 + 4} \ $$ = \sqrt{8} = 2\sqrt{2}$ units.
$CD = \sqrt{(-3 - (-1))^2 + (0 - 2)^2} = \sqrt{(-2)^2 + (-2)^2} = \sqrt{4 + 4} \ $$ = \sqrt{8} = 2\sqrt{2}$ units.
$DA = \sqrt{(-1 - (-3))^2 + (-2 - 0)^2} = \sqrt{(2)^2 + (-2)^2} = \sqrt{4 + 4} \ $$ = \sqrt{8} = 2\sqrt{2}$ units.
Since all four sides are equal ($AB = BC = CD = DA$), the quadrilateral is either a rhombus or a square.
Length of the diagonals:
$AC = \sqrt{(-1 - (-1))^2 + (2 - (-2))^2} = \sqrt{(0)^2 + (4)^2} = \sqrt{16} = 4$ units.
$BD = \sqrt{(-3 - 1)^2 + (0 - 0)^2} = \sqrt{(-4)^2 + (0)^2} = \sqrt{16} = 4$ units.
Since the diagonals are also equal ($AC = BD$), the quadrilateral is a square.
Therefore, the points (– 1, – 2), (1, 0), (– 1, 2), and (– 3, 0) form a square.
(ii) (–3, 5), (3, 1), (0, 3), (–1, – 4)
Solution
Let the given points be A(–3, 5), B(3, 1), C(0, 3), and D(–1, –4).
Let's find the distances between some of these points.
$AB = \sqrt{(3 - (-3))^2 + (1 - 5)^2} = \sqrt{(6)^2 + (-4)^2} = \sqrt{36 + 16} \ $$ = \sqrt{52} = 2\sqrt{13}$ units.
$BC = \sqrt{(0 - 3)^2 + (3 - 1)^2} = \sqrt{(-3)^2 + (2)^2} = \sqrt{9 + 4} \ $$ = \sqrt{13}$ units.
$AC = \sqrt{(0 - (-3))^2 + (3 - 5)^2} = \sqrt{(3)^2 + (-2)^2} = \sqrt{9 + 4} \ $$ = \sqrt{13}$ units.
Here, we observe that:
$AC + BC = \sqrt{13} + \sqrt{13} = 2\sqrt{13}$
And the length of the segment AB is $2\sqrt{13}$.
Since $AC + BC = AB$, the points A, C, and B are collinear (i.e., they lie on the same straight line).
Therefore, the given points do not form a quadrilateral.
(iii) (4, 5), (7, 6), (4, 3), (1, 2)
Solution
Let the given points be A(4, 5), B(7, 6), C(4, 3), and D(1, 2).
We find the lengths of the four sides and both diagonals.
Length of the sides:
$AB = \sqrt{(7 - 4)^2 + (6 - 5)^2} = \sqrt{(3)^2 + (1)^2} = \sqrt{9 + 1} = \sqrt{10}$ units.
$BC = \sqrt{(4 - 7)^2 + (3 - 6)^2} = \sqrt{(-3)^2 + (-3)^2} = \sqrt{9 + 9} = \sqrt{18} \ $$ = 3\sqrt{2}$ units.
$CD = \sqrt{(1 - 4)^2 + (2 - 3)^2} = \sqrt{(-3)^2 + (-1)^2} = \sqrt{9 + 1} = \sqrt{10}$ units.
$DA = \sqrt{(4 - 1)^2 + (5 - 2)^2} = \sqrt{(3)^2 + (3)^2} = \sqrt{9 + 9} = \sqrt{18} \ $$ = 3\sqrt{2}$ units.
Here, the opposite sides are equal: $AB = CD = \sqrt{10}$ and $BC = DA = \sqrt{18}$. So, the quadrilateral is either a parallelogram or a rectangle.
Length of the diagonals:
$AC = \sqrt{(4 - 4)^2 + (3 - 5)^2} = \sqrt{(0)^2 + (-2)^2} = \sqrt{4} = 2$ units.
$BD = \sqrt{(1 - 7)^2 + (2 - 6)^2} = \sqrt{(-6)^2 + (-4)^2} = \sqrt{36 + 16} \ $$ = \sqrt{52} = 2\sqrt{13}$ units.
Since the diagonals are not equal ($AC \neq BD$), the quadrilateral is not a rectangle.
Therefore, as the opposite sides are equal and diagonals are unequal, the points (4, 5), (7, 6), (4, 3), and (1, 2) form a parallelogram.
Question 7. Find the point on the x-axis which is equidistant from (2, –5) and (–2, 9).
Answer:
Given:
Two points $A(2, -5)$ and $B(-2, 9)$.
We need to find a point on the x-axis which is equidistant from A and B.
To Find:
The coordinates of the point on the x-axis equidistant from A and B.
Solution:
Let the point on the x-axis be $P(x, 0)$. Since any point on the x-axis has its y-coordinate as 0.
We are given that the point P is equidistant from points A and B. Therefore, $PA = PB$.
Using the distance formula, the distance between two points $(x_1, y_1)$ and $(x_2, y_2)$ is $\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$.
Calculating the distance PA:
$PA = \sqrt{(2 - x)^2 + (-5 - 0)^2}$
$PA = \sqrt{(2 - x)^2 + (-5)^2}$
$PA = \sqrt{(2 - x)^2 + 25}$
Calculating the distance PB:
$PB = \sqrt{(-2 - x)^2 + (9 - 0)^2}$
$PB = \sqrt{(-(2 + x))^2 + (9)^2}$
$PB = \sqrt{(2 + x)^2 + 81}$
Since $PA = PB$, we have $PA^2 = PB^2$.
$\left(\sqrt{(2 - x)^2 + 25}\right)^2 = \left(\sqrt{(2 + x)^2 + 81}\right)^2$
$(2 - x)^2 + 25 = (2 + x)^2 + 81$
Expanding the squared terms:
$(4 - 4x + x^2) + 25 = (4 + 4x + x^2) + 81$
$x^2 - 4x + 29 = x^2 + 4x + 85$
Subtract $x^2$ from both sides:
$-4x + 29 = 4x + 85$
Rearrange the terms to solve for $x$:
$29 - 85 = 4x + 4x$
$-56 = 8x$
$x = \frac{-56}{8}$
$x = -7$
So, the coordinates of the point P on the x-axis are $(x, 0) = (-7, 0)$.
Therefore, the required point on the x-axis is (-7, 0).
Question 8. Find the values of y for which the distance between the points P(2, – 3) and Q(10, y) is 10 units.
Answer:
Given:
Two points $P(2, -3)$ and $Q(10, y)$.
The distance between P and Q is 10 units, i.e., $PQ = 10$.
To Find:
The possible values of $y$.
Solution:
We use the distance formula: The distance between two points $(x_1, y_1)$ and $(x_2, y_2)$ is $d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$.
Here, $(x_1, y_1) = (2, -3)$ and $(x_2, y_2) = (10, y)$, and $d = 10$.
Substituting these values into the distance formula:
$10 = \sqrt{(10 - 2)^2 + (y - (-3))^2}$
Simplify the expression inside the square root:
$10 = \sqrt{(8)^2 + (y + 3)^2}$
$10 = \sqrt{64 + (y + 3)^2}$
To eliminate the square root, square both sides of the equation:
$10^2 = \left(\sqrt{64 + (y + 3)^2}\right)^2$
$100 = 64 + (y + 3)^2$
Isolate the term $(y + 3)^2$:
$(y + 3)^2 = 100 - 64$
$(y + 3)^2 = 36$
Take the square root of both sides:
$\sqrt{(y + 3)^2} = \sqrt{36}$
$y + 3 = \pm 6$
We have two possible cases:
Case 1: $y + 3 = 6$
$y = 6 - 3$
$y = 3$
Case 2: $y + 3 = -6$
$y = -6 - 3$
$y = -9$
Therefore, the possible values of $y$ for which the distance between P(2, –3) and Q(10, y) is 10 units are 3 and –9.
Question 9. If Q(0, 1) is equidistant from P(5,–3) and R(x,6), find the values of x. Also find the distances QR and PR.
Answer:
Given:
Points $P(5, -3)$, $Q(0, 1)$, and $R(x, 6)$.
Point Q is equidistant from P and R, which means $QP = QR$.
To Find:
1. The value(s) of $x$.
2. The distances QR and PR.
Solution:
Since Q is equidistant from P and R, we have $QP = QR$.
This implies $QP^2 = QR^2$.
We use the distance formula $d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$, or $d^2 = (x_2 - x_1)^2 + (y_2 - y_1)^2$.
Calculating $QP^2$:
Points are $Q(0, 1)$ and $P(5, -3)$.
$QP^2 = (5 - 0)^2 + (-3 - 1)^2$
$QP^2 = (5)^2 + (-4)^2$
$QP^2 = 25 + 16 = 41$
Calculating $QR^2$:
Points are $Q(0, 1)$ and $R(x, 6)$.
$QR^2 = (x - 0)^2 + (6 - 1)^2$
$QR^2 = x^2 + (5)^2$
$QR^2 = x^2 + 25$
Now, setting $QP^2 = QR^2$:
$41 = x^2 + 25$
$x^2 = 41 - 25$
$x^2 = 16$
$x = \pm \sqrt{16}$
$x = 4$ or $x = -4$.
So, the possible values of $x$ are 4 and -4.
The point R can be either $(4, 6)$ or $(-4, 6)$.
Finding the distance QR:
We know $QR^2 = x^2 + 25$. Since $x^2 = 16$,
$QR^2 = 16 + 25 = 41$
$QR = \sqrt{41}$ units.
The distance QR is $\sqrt{41}$ units (this is true for both $x=4$ and $x=-4$).
Finding the distance PR:
We need to calculate PR for both possible coordinates of R.
Case 1: R is $(4, 6)$
Points are $P(5, -3)$ and $R(4, 6)$.
$PR = \sqrt{(4 - 5)^2 + (6 - (-3))^2}$
$PR = \sqrt{(-1)^2 + (6 + 3)^2}$
$PR = \sqrt{1^2 + 9^2}$
$PR = \sqrt{1 + 81} = \sqrt{82}$ units.
Case 2: R is $(-4, 6)$
Points are $P(5, -3)$ and $R(-4, 6)$.
$PR = \sqrt{(-4 - 5)^2 + (6 - (-3))^2}$
$PR = \sqrt{(-9)^2 + (6 + 3)^2}$
$PR = \sqrt{(-9)^2 + 9^2}$
$PR = \sqrt{81 + 81} = \sqrt{162}$
$PR = \sqrt{81 \times 2} = 9\sqrt{2}$ units.
Thus, the distances PR are $\sqrt{82}$ units or $9\sqrt{2}$ units.
Question 10. Find a relation between x and y such that the point (x, y) is equidistant from the point (3, 6) and (– 3, 4).
Answer:
Given:
Let $P(x, y)$ be a point that is equidistant from the points $A(3, 6)$ and $B(-3, 4)$.
To Find:
A relation between $x$ and $y$.
Solution:
Since point $P(x, y)$ is equidistant from points $A(3, 6)$ and $B(-3, 4)$, the distance $PA$ must be equal to the distance $PB$.
We use the distance formula: The distance between two points $(x_1, y_1)$ and $(x_2, y_2)$ is $\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$.
Calculating the distance PA:
$PA = \sqrt{(3 - x)^2 + (6 - y)^2}$
Calculating the distance PB:
$PB = \sqrt{(-3 - x)^2 + (4 - y)^2}$
According to the given condition, $PA = PB$.
This implies $PA^2 = PB^2$. Squaring both sides eliminates the square roots:
$(3 - x)^2 + (6 - y)^2 = (-3 - x)^2 + (4 - y)^2$
Expand the terms:
$(9 - 6x + x^2) + (36 - 12y + y^2) = ((-1)(3 + x))^2 + (16 - 8y + y^2)$
$x^2 - 6x + y^2 - 12y + 9 + 36 = (3 + x)^2 + y^2 - 8y + 16$
$x^2 - 6x + y^2 - 12y + 45 = (9 + 6x + x^2) + y^2 - 8y + 16$
$x^2 - 6x + y^2 - 12y + 45 = x^2 + 6x + y^2 - 8y + 25$
Subtract $x^2$ and $y^2$ from both sides:
$-6x - 12y + 45 = 6x - 8y + 25$
Rearrange the terms to bring variables to one side and constants to the other:
$45 - 25 = 6x + 6x - 8y + 12y$
$20 = 12x + 4y$
Divide the entire equation by the greatest common divisor, which is 4:
$\frac{20}{4} = \frac{12x}{4} + \frac{4y}{4}$
$5 = 3x + y$
This can also be written as $3x + y - 5 = 0$.
Therefore, the required relation between $x$ and $y$ is $3x + y = 5$.
Example 6 to 10 (Before Exercise 7.2)
Example 6. Find the coordinates of the point which divides the line segment joining the points (4, – 3) and (8, 5) in the ratio 3 : 1 internally.
Answer:
Given:
The line segment joins the points $A(4, -3)$ and $B(8, 5)$.
The ratio of internal division is $m_1 : m_2 = 3 : 1$.
To Find:
The coordinates of the point which divides the line segment AB internally in the ratio 3 : 1.
Solution:
Let $P(x, y)$ be the point that divides the line segment joining $A(x_1, y_1) = (4, -3)$ and $B(x_2, y_2) = (8, 5)$ internally in the ratio $m_1 : m_2 = 3 : 1$.
We use the section formula for internal division:
$x = \frac{m_1 x_2 + m_2 x_1}{m_1 + m_2}$
$y = \frac{m_1 y_2 + m_2 y_1}{m_1 + m_2}$
Substitute the given values:
$x_1 = 4$, $y_1 = -3$
$x_2 = 8$, $y_2 = 5$
$m_1 = 3$, $m_2 = 1$
Calculating the x-coordinate:
$x = \frac{3(8) + 1(4)}{3 + 1}$
$x = \frac{24 + 4}{4}$
$x = \frac{28}{4}$
$x = 7$
Calculating the y-coordinate:
$y = \frac{3(5) + 1(-3)}{3 + 1}$
$y = \frac{15 - 3}{4}$
$y = \frac{12}{4}$
$y = 3$
So, the coordinates of the point P are $(7, 3)$.
Therefore, the coordinates of the point which divides the line segment joining the points (4, – 3) and (8, 5) in the ratio 3 : 1 internally are (7, 3).
Example 7. In what ratio does the point (– 4, 6) divide the line segment joining the points A(– 6, 10) and B(3, – 8)?
Answer:
Given:
The line segment is formed by joining points $A(-6, 10)$ and $B(3, -8)$.
The point $P(-4, 6)$ divides this line segment.
To Find:
The ratio in which the point P divides the line segment AB.
Solution:
Let the point $P(-4, 6)$ divide the line segment joining $A(x_1, y_1) = (-6, 10)$ and $B(x_2, y_2) = (3, -8)$ in the ratio $m_1 : m_2$.
Using the section formula for internal division, the coordinates of the point P are given by:
$x = \frac{m_1 x_2 + m_2 x_1}{m_1 + m_2}$
$y = \frac{m_1 y_2 + m_2 y_1}{m_1 + m_2}$
We are given the coordinates of P as $(-4, 6)$. We can use either the x-coordinate or the y-coordinate formula to find the ratio.
Using the x-coordinate:
$x = -4$
$-4 = \frac{m_1(3) + m_2(-6)}{m_1 + m_2}$
Multiply both sides by $(m_1 + m_2)$:
$-4(m_1 + m_2) = 3m_1 - 6m_2$
$-4m_1 - 4m_2 = 3m_1 - 6m_2$
Rearrange the terms to group $m_1$ and $m_2$:
$-4m_2 + 6m_2 = 3m_1 + 4m_1$
$2m_2 = 7m_1$
To find the ratio $m_1 : m_2$, we rearrange the equation:
$\frac{m_1}{m_2} = \frac{2}{7}$
So, the ratio $m_1 : m_2$ is $2 : 7$.
Alternate Solution (using the y-coordinate):
We use the y-coordinate formula:
$y = 6$
$6 = \frac{m_1(-8) + m_2(10)}{m_1 + m_2}$
Multiply both sides by $(m_1 + m_2)$:
$6(m_1 + m_2) = -8m_1 + 10m_2$
$6m_1 + 6m_2 = -8m_1 + 10m_2$
Rearrange the terms:
$6m_1 + 8m_1 = 10m_2 - 6m_2$
$14m_1 = 4m_2$
Rearrange to find the ratio $m_1 : m_2$:
$\frac{m_1}{m_2} = \frac{4}{14}$
Simplify the fraction:
$\frac{m_1}{m_2} = \frac{2}{7}$
The ratio $m_1 : m_2$ is $2 : 7$.
Both methods yield the same result.
Therefore, the point (– 4, 6) divides the line segment joining the points A(– 6, 10) and B(3, – 8) in the ratio 2 : 7.
Example 8. Find the coordinates of the points of trisection (i.e., points dividing in three equal parts) of the line segment joining the points A(2, – 2) and B(– 7, 4).
Answer:
Given
The line segment joining the points A(2, – 2) and B(– 7, 4).
To Find
The coordinates of the points of trisection of the line segment AB.
Solution
Let P and Q be the points of trisection of the line segment joining A(2, – 2) and B(– 7, 4).
This means that the points P and Q divide the line segment AB into three equal parts, i.e., $AP = PQ = QB$.
From the figure, we can see that point P divides the line segment AB in the ratio 1:2.
Similarly, point Q divides the line segment AB in the ratio 2:1.
We will use the section formula to find the coordinates. The coordinates of a point $(x, y)$ that divides the line segment joining points $(x_1, y_1)$ and $(x_2, y_2)$ internally in the ratio $m_1:m_2$ are given by:
$x = \frac{m_1x_2 + m_2x_1}{m_1 + m_2}$ and $y = \frac{m_1y_2 + m_2y_1}{m_1 + m_2}$
Coordinates of P
Point P divides AB in the ratio 1:2. So, $m_1 = 1$ and $m_2 = 2$.
Here, $(x_1, y_1) = (2, -2)$ and $(x_2, y_2) = (-7, 4)$.
The x-coordinate of P is:
$x = \frac{1(-7) + 2(2)}{1+2} = \frac{-7 + 4}{3} = \frac{-3}{3} = -1$
The y-coordinate of P is:
$y = \frac{1(4) + 2(-2)}{1+2} = \frac{4 - 4}{3} = \frac{0}{3} = 0$
So, the coordinates of point P are (–1, 0).
Coordinates of Q
Point Q divides AB in the ratio 2:1. So, $m_1 = 2$ and $m_2 = 1$.
The x-coordinate of Q is:
$x = \frac{2(-7) + 1(2)}{2+1} = \frac{-14 + 2}{3} = \frac{-12}{3} = -4$
The y-coordinate of Q is:
$y = \frac{2(4) + 1(-2)}{2+1} = \frac{8 - 2}{3} = \frac{6}{3} = 2$
So, the coordinates of point Q are (–4, 2).
Thus, the required coordinates of the points of trisection of the line segment AB are (–1, 0) and (–4, 2).
Alternate Solution
First, we find the coordinates of point P, which divides AB in the ratio 1:2. As calculated above, the coordinates of P are (–1, 0).
Now, observe that Q is the midpoint of the line segment PB.
The coordinates of P are (–1, 0) and the coordinates of B are (–7, 4).
We can use the midpoint formula to find the coordinates of Q:
$Q = \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right)$
Substituting the coordinates of P and B:
$Q = \left( \frac{-1 + (-7)}{2}, \frac{0 + 4}{2} \right)$
$Q = \left( \frac{-8}{2}, \frac{4}{2} \right)$
$Q = (-4, 2)$
This confirms our previous result. The coordinates of the points of trisection are (–1, 0) and (–4, 2).
Example 9. Find the ratio in which the y-axis divides the line segment joining the points (5, – 6) and (–1, – 4). Also find the point of intersection.
Answer:
Given:
The line segment joins the points $A(5, -6)$ and $B(-1, -4)$.
This line segment is divided by the y-axis.
To Find:
1. The ratio in which the y-axis divides the line segment AB.
2. The coordinates of the point of intersection.
Solution:
Let the y-axis divide the line segment joining $A(5, -6)$ and $B(-1, -4)$ in the ratio $m_1 : m_2$.
Let the point of intersection on the y-axis be $P(x, y)$. Since the point lies on the y-axis, its x-coordinate must be 0. So, the point of intersection is $P(0, y)$.
Using the section formula, the coordinates of the point P dividing the line segment joining $(x_1, y_1) = (5, -6)$ and $(x_2, y_2) = (-1, -4)$ in the ratio $m_1 : m_2$ are given by:
$x = \frac{m_1 x_2 + m_2 x_1}{m_1 + m_2}$
$y = \frac{m_1 y_2 + m_2 y_1}{m_1 + m_2}$
We know the x-coordinate of the intersection point P is 0. So, we use the formula for the x-coordinate:
$0 = \frac{m_1(-1) + m_2(5)}{m_1 + m_2}$
Multiply both sides by $(m_1 + m_2)$:
$0 \times (m_1 + m_2) = -m_1 + 5m_2$
$0 = -m_1 + 5m_2$
$m_1 = 5m_2$
Rearrange to find the ratio $m_1 : m_2$:
$\frac{m_1}{m_2} = \frac{5}{1}$
Therefore, the ratio in which the y-axis divides the line segment is $5 : 1$.
Now, we find the coordinates of the point of intersection P(0, y) using the formula for the y-coordinate and the ratio $m_1 = 5$, $m_2 = 1$.
$y = \frac{m_1 y_2 + m_2 y_1}{m_1 + m_2}$
$y = \frac{5(-4) + 1(-6)}{5 + 1}$
$y = \frac{-20 - 6}{6}$
$y = \frac{-26}{6}$
Simplify the fraction:
$y = -\frac{13}{3}$
So, the coordinates of the point of intersection are $(0, y) = (0, -13/3)$.
Therefore, the point of intersection is $(0, -13/3)$.
Example 10. If the points A(6, 1), B(8, 2), C(9, 4) and D(p, 3) are the vertices of a parallelogram, taken in order, find the value of p.
Answer:
Given:
The points $A(6, 1)$, $B(8, 2)$, $C(9, 4)$, and $D(p, 3)$ are the vertices of a parallelogram ABCD, taken in order.
To Find:
The value of $p$.
Solution:
We know that the diagonals of a parallelogram bisect each other. This means that the midpoint of the diagonal AC is the same as the midpoint of the diagonal BD.
The midpoint formula for a line segment joining points $(x_1, y_1)$ and $(x_2, y_2)$ is given by:
$M = \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right)$
Midpoint of diagonal AC:
Using points $A(6, 1)$ and $C(9, 4)$: $(x_1, y_1) = (6, 1)$, $(x_2, y_2) = (9, 4)$.
Midpoint of AC = $\left( \frac{6 + 9}{2}, \frac{1 + 4}{2} \right) = \left( \frac{15}{2}, \frac{5}{2} \right)$
Midpoint of diagonal BD:
Using points $B(8, 2)$ and $D(p, 3)$: $(x_1, y_1) = (8, 2)$, $(x_2, y_2) = (p, 3)$.
Midpoint of BD = $\left( \frac{8 + p}{2}, \frac{2 + 3}{2} \right) = \left( \frac{8 + p}{2}, \frac{5}{2} \right)$
Since the midpoints of AC and BD are the same point:
$\left( \frac{15}{2}, \frac{5}{2} \right) = \left( \frac{8 + p}{2}, \frac{5}{2} \right)$
Equating the x-coordinates:
$\frac{15}{2} = \frac{8 + p}{2}$
Multiply both sides by 2:
$15 = 8 + p$
Solve for $p$:
$p = 15 - 8$
$p = 7$
(Equating the y-coordinates, $\frac{5}{2} = \frac{5}{2}$, which is consistent.)
Therefore, the value of $p$ is 7.
Exercise 7.2
Question 1. Find the coordinates of the point which divides the join of (–1,7) and (4,–3) in the ratio 2 : 3.
Answer:
Given:
The line segment joins the points $A(-1, 7)$ and $B(4, -3)$.
The ratio of internal division is $m_1 : m_2 = 2 : 3$.
To Find:
The coordinates of the point which divides the line segment AB internally in the ratio 2 : 3.
Solution:
Let $P(x, y)$ be the point that divides the line segment joining $A(x_1, y_1) = (-1, 7)$ and $B(x_2, y_2) = (4, -3)$ internally in the ratio $m_1 : m_2 = 2 : 3$.
We use the section formula for internal division:
$x = \frac{m_1 x_2 + m_2 x_1}{m_1 + m_2}$
$y = \frac{m_1 y_2 + m_2 y_1}{m_1 + m_2}$
Substitute the given values:
$x_1 = -1$, $y_1 = 7$
$x_2 = 4$, $y_2 = -3$
$m_1 = 2$, $m_2 = 3$
Calculating the x-coordinate:
$x = \frac{2(4) + 3(-1)}{2 + 3}$
$x = \frac{8 - 3}{5}$
$x = \frac{5}{5}$
$x = 1$
Calculating the y-coordinate:
$y = \frac{2(-3) + 3(7)}{2 + 3}$
$y = \frac{-6 + 21}{5}$
$y = \frac{15}{5}$
$y = 3$
So, the coordinates of the point P are $(1, 3)$.
Therefore, the coordinates of the point which divides the join of (–1, 7) and (4, –3) in the ratio 2 : 3 are (1, 3).
Question 2. Find the coordinates of the points of trisection of the line segment joining (4,–1) and (–2,–3).
Answer:
Given:
The line segment joins the points $A(4, -1)$ and $B(-2, -3)$.
We need to find the points of trisection.
To Find:
The coordinates of the two points that divide the line segment AB into three equal parts.
Solution:
Let P and Q be the points of trisection of the line segment joining $A(4, -1)$ and $B(-2, -3)$.
This means that AP = PQ = QB.
Point P divides the line segment AB internally in the ratio $AP : PB = 1 : (PQ + QB) = 1 : (1 + 1) = 1 : 2$.
Point Q divides the line segment AB internally in the ratio $AQ : QB = (AP + PQ) : 1 = (1 + 1) : 1 = 2 : 1$.
We use the section formula to find the coordinates of P and Q. The coordinates $(x, y)$ of a point dividing the line segment joining $(x_1, y_1)$ and $(x_2, y_2)$ internally in the ratio $m_1 : m_2$ are:
$x = \frac{m_1 x_2 + m_2 x_1}{m_1 + m_2}$
$y = \frac{m_1 y_2 + m_2 y_1}{m_1 + m_2}$
Coordinates of P (dividing AB in the ratio 1 : 2):
Here, $(x_1, y_1) = (4, -1)$, $(x_2, y_2) = (-2, -3)$, $m_1 = 1$, $m_2 = 2$.
$x_P = \frac{1(-2) + 2(4)}{1 + 2} = \frac{-2 + 8}{3} = \frac{6}{3} = 2$
$y_P = \frac{1(-3) + 2(-1)}{1 + 2} = \frac{-3 - 2}{3} = \frac{-5}{3}$
So, the coordinates of point P are $(2, -5/3)$.
Coordinates of Q (dividing AB in the ratio 2 : 1):
Here, $(x_1, y_1) = (4, -1)$, $(x_2, y_2) = (-2, -3)$, $m_1 = 2$, $m_2 = 1$.
$x_Q = \frac{2(-2) + 1(4)}{2 + 1} = \frac{-4 + 4}{3} = \frac{0}{3} = 0$
$y_Q = \frac{2(-3) + 1(-1)}{2 + 1} = \frac{-6 - 1}{3} = \frac{-7}{3}$
So, the coordinates of point Q are $(0, -7/3)$.
Therefore, the coordinates of the points of trisection of the line segment joining (4, –1) and (–2, –3) are $(2, -5/3)$ and $(0, -7/3)$.
Question 3. To conduct Sports Day activities, in your rectangular shaped school ground ABCD, lines have been drawn with chalk powder at a distance of 1m each. 100 flower pots have been placed at a distance of 1m from each other along AD, as shown in Fig. 7.12. Niharika runs $\frac{1}{4}$ th the distance AD on the 2nd line and posts a green flag. Preet runs $\frac{1}{5}$ th the distance AD on the eighth line and posts a red flag. What is the distance between both the flags? If Rashmi has to post a blue flag exactly halfway between the line segment joining the two flags, where should she post her flag?

Answer:
Given:
Let the rectangular ground be represented on a coordinate plane with AD along the y-axis and AB along the x-axis. The lines are 1m apart, so the line numbers correspond to the x-coordinates.
The total distance along AD is 100 m (100 flower pots at 1m distance).
Niharika runs on the 2nd line (x = 2).
Distance covered by Niharika along AD = $\frac{1}{4} \times 100 = 25$ m.
Coordinates of the green flag posted by Niharika (let's call this point G) are $(2, 25)$.
Preet runs on the 8th line (x = 8).
Distance covered by Preet along AD = $\frac{1}{5} \times 100 = 20$ m.
Coordinates of the red flag posted by Preet (let's call this point R) are $(8, 20)$.
To Find:
1. The distance between the green flag (G) and the red flag (R).
2. The coordinates where Rashmi should post her blue flag, which is exactly halfway between G and R.
Solution:
1. Distance between the flags (GR):
We use the distance formula to find the distance between G(2, 25) and R(8, 20).
$d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$
$GR = \sqrt{(8 - 2)^2 + (20 - 25)^2}$
$GR = \sqrt{(6)^2 + (-5)^2}$
$GR = \sqrt{36 + 25}$
$GR = \sqrt{61}$ m.
The distance between both the flags is $\sqrt{61}$ m.
2. Position of the blue flag (Midpoint of GR):
Rashmi posts her blue flag exactly halfway between the line segment joining G(2, 25) and R(8, 20). Let the coordinates of this point be M(x, y).
We use the midpoint formula:
$M(x, y) = \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right)$
$x = \frac{2 + 8}{2} = \frac{10}{2} = 5$
$y = \frac{25 + 20}{2} = \frac{45}{2} = 22.5$
The coordinates of the point where Rashmi should post her blue flag are $(5, 22.5)$.
This means Rashmi should post her flag on the 5th line at a distance of 22.5 m from the starting point along the line AD.
Question 4. Find the ratio in which the line segment joining the points (– 3, 10) and (6, – 8) is divided by (– 1, 6).
Answer:
Given:
The line segment joins the points $A(-3, 10)$ and $B(6, -8)$.
The point $P(-1, 6)$ divides this line segment.
To Find:
The ratio in which the point P divides the line segment AB.
Solution:
Let the point $P(-1, 6)$ divide the line segment joining $A(x_1, y_1) = (-3, 10)$ and $B(x_2, y_2) = (6, -8)$ in the ratio $m_1 : m_2$.
Using the section formula for internal division, the coordinates of the point P are given by:
$x = \frac{m_1 x_2 + m_2 x_1}{m_1 + m_2}$
$y = \frac{m_1 y_2 + m_2 y_1}{m_1 + m_2}$
We are given the coordinates of P as $(-1, 6)$. We can use either the x-coordinate or the y-coordinate formula to find the ratio.
Using the x-coordinate:
$x = -1$
$-1 = \frac{m_1(6) + m_2(-3)}{m_1 + m_2}$
Multiply both sides by $(m_1 + m_2)$:
$-1(m_1 + m_2) = 6m_1 - 3m_2$
$-m_1 - m_2 = 6m_1 - 3m_2$
Rearrange the terms to group $m_1$ and $m_2$:
$-m_2 + 3m_2 = 6m_1 + m_1$
$2m_2 = 7m_1$
To find the ratio $m_1 : m_2$, we rearrange the equation:
$\frac{m_1}{m_2} = \frac{2}{7}$
So, the ratio $m_1 : m_2$ is $2 : 7$.
Alternate Solution (using the y-coordinate):
Using the y-coordinate:
$y = 6$
$6 = \frac{m_1(-8) + m_2(10)}{m_1 + m_2}$
Multiply both sides by $(m_1 + m_2)$:
$6(m_1 + m_2) = -8m_1 + 10m_2$
$6m_1 + 6m_2 = -8m_1 + 10m_2$
Rearrange the terms:
$6m_1 + 8m_1 = 10m_2 - 6m_2$
$14m_1 = 4m_2$
Rearrange to find the ratio $m_1 : m_2$:
$\frac{m_1}{m_2} = \frac{4}{14}$
Simplify the fraction:
$\frac{m_1}{m_2} = \frac{2}{7}$
The ratio $m_1 : m_2$ is $2 : 7$.
Both methods yield the same result.
Therefore, the point (– 1, 6) divides the line segment joining the points (– 3, 10) and (6, – 8) in the ratio 2 : 7.
Question 5. Find the ratio in which the line segment joining A(1, – 5) and B(– 4, 5) is divided by the x-axis. Also find the coordinates of the point of division.
Answer:
Given:
The line segment joins the points $A(1, -5)$ and $B(-4, 5)$.
This line segment is divided by the x-axis.
To Find:
1. The ratio in which the x-axis divides the line segment AB.
2. The coordinates of the point of division.
Solution:
Let the x-axis divide the line segment joining $A(1, -5)$ and $B(-4, 5)$ in the ratio $m_1 : m_2$.
Let the point of intersection on the x-axis be $P(x, y)$. Since the point lies on the x-axis, its y-coordinate must be 0. So, the point of intersection is $P(x, 0)$.
Using the section formula, the coordinates of the point P dividing the line segment joining $(x_1, y_1) = (1, -5)$ and $(x_2, y_2) = (-4, 5)$ in the ratio $m_1 : m_2$ are given by:
$x = \frac{m_1 x_2 + m_2 x_1}{m_1 + m_2}$
$y = \frac{m_1 y_2 + m_2 y_1}{m_1 + m_2}$
We know the y-coordinate of the intersection point P is 0. So, we use the formula for the y-coordinate:
$0 = \frac{m_1(5) + m_2(-5)}{m_1 + m_2}$
Multiply both sides by $(m_1 + m_2)$:
$0 \times (m_1 + m_2) = 5m_1 - 5m_2$
$0 = 5m_1 - 5m_2$
$5m_1 = 5m_2$
Rearrange to find the ratio $m_1 : m_2$:
$\frac{m_1}{m_2} = \frac{5}{5} = \frac{1}{1}$
Therefore, the ratio in which the x-axis divides the line segment is $1 : 1$.
Now, we find the coordinates of the point of division P(x, 0) using the formula for the x-coordinate and the ratio $m_1 = 1$, $m_2 = 1$.
$x = \frac{m_1 x_2 + m_2 x_1}{m_1 + m_2}$
$x = \frac{1(-4) + 1(1)}{1 + 1}$
$x = \frac{-4 + 1}{2}$
$x = \frac{-3}{2}$
So, the x-coordinate is $-3/2$, and the y-coordinate is 0.
Therefore, the coordinates of the point of division are $(-3/2, 0)$.
(Note: Since the ratio is 1:1, the point of division is the midpoint of the line segment AB.)
Question 6. If (1, 2), (4, y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find x and y.
Answer:
Given:
Let the vertices of the parallelogram, taken in order, be $A(1, 2)$, $B(4, y)$, $C(x, 6)$, and $D(3, 5)$.
To Find:
The values of $x$ and $y$.
Solution:
We know that the diagonals of a parallelogram bisect each other. This means the midpoint of diagonal AC is the same as the midpoint of diagonal BD.
The midpoint formula for a line segment joining points $(x_1, y_1)$ and $(x_2, y_2)$ is given by:
$M = \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right)$
Midpoint of diagonal AC:
Using points $A(1, 2)$ and $C(x, 6)$:
Midpoint of AC = $\left( \frac{1 + x}{2}, \frac{2 + 6}{2} \right) = \left( \frac{1 + x}{2}, \frac{8}{2} \right) = \left( \frac{1 + x}{2}, 4 \right)$
Midpoint of diagonal BD:
Using points $B(4, y)$ and $D(3, 5)$:
Midpoint of BD = $\left( \frac{4 + 3}{2}, \frac{y + 5}{2} \right) = \left( \frac{7}{2}, \frac{y + 5}{2} \right)$
Since the midpoints of AC and BD must be the same point for a parallelogram:
Midpoint of AC = Midpoint of BD
$\left( \frac{1 + x}{2}, 4 \right) = \left( \frac{7}{2}, \frac{y + 5}{2} \right)$
Equating the corresponding coordinates:
Equating the x-coordinates:
$\frac{1 + x}{2} = \frac{7}{2}$
Multiply both sides by 2:
$1 + x = 7$
$x = 7 - 1$
$x = 6$
Equating the y-coordinates:
$4 = \frac{y + 5}{2}$
Multiply both sides by 2:
$8 = y + 5$
$y = 8 - 5$
$y = 3$
Therefore, the values are $x = 6$ and $y = 3$.
Question 7. Find the coordinates of a point A, where AB is the diameter of a circle whose centre is (2, – 3) and B is (1, 4).
Answer:
Given:
AB is the diameter of a circle.
The coordinates of the centre of the circle (let's call it C) are $(2, -3)$.
The coordinates of point B are $(1, 4)$.
To Find:
The coordinates of point A.
Solution:
Let the coordinates of point A be $(x, y)$.
Since AB is the diameter of the circle, the centre C must be the midpoint of the diameter AB.
We use the midpoint formula. The midpoint of a line segment joining points $(x_1, y_1)$ and $(x_2, y_2)$ is given by:
$M = \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right)$
Here, the midpoint is the centre $C(2, -3)$, and the endpoints of the diameter are $A(x, y)$ and $B(1, 4)$.
Applying the midpoint formula to the segment AB:
Coordinates of C = $\left( \frac{x + 1}{2}, \frac{y + 4}{2} \right)$
We are given that the coordinates of the centre C are $(2, -3)$. Therefore, we can equate the coordinates:
Equating the x-coordinates:
$\frac{x + 1}{2} = 2$
Multiply both sides by 2:
$x + 1 = 4$
$x = 4 - 1$
$x = 3$
Equating the y-coordinates:
$\frac{y + 4}{2} = -3$
Multiply both sides by 2:
$y + 4 = -6$
$y = -6 - 4$
$y = -10$
So, the coordinates of point A are $(x, y) = (3, -10)$.
Therefore, the coordinates of point A are (3, -10).
Question 8. If A and B are (– 2, – 2) and (2, – 4), respectively , find the coordinates of P such that AP = $\frac{3}{7}$ AB and P lies on the line segment AB.
Answer:
Given:
The coordinates of points A and B are $A(-2, -2)$ and $B(2, -4)$.
Point P lies on the line segment AB.
The condition $AP = \frac{3}{7} AB$ holds.
To Find:
The coordinates of point P.
Solution:
Since P lies on the line segment AB, it divides AB internally.
We are given $AP = \frac{3}{7} AB$.
We can find the length of the segment PB:
$PB = AB - AP$
$PB = AB - \frac{3}{7} AB$
$PB = \left(1 - \frac{3}{7}\right) AB$
$PB = \frac{7 - 3}{7} AB = \frac{4}{7} AB$
Now, we find the ratio in which P divides AB, which is $AP : PB$.
$AP : PB = \frac{3}{7} AB : \frac{4}{7} AB$
Dividing both parts by $\frac{1}{7} AB$, we get the ratio:
$AP : PB = 3 : 4$
So, point P divides the line segment AB internally in the ratio $m_1 : m_2 = 3 : 4$.
Let the coordinates of A be $(x_1, y_1) = (-2, -2)$ and the coordinates of B be $(x_2, y_2) = (2, -4)$.
Let the coordinates of P be $(x, y)$.
Using the section formula for internal division:
$x = \frac{m_1 x_2 + m_2 x_1}{m_1 + m_2}$
$y = \frac{m_1 y_2 + m_2 y_1}{m_1 + m_2}$
Substitute the values $m_1 = 3$, $m_2 = 4$, $x_1 = -2$, $y_1 = -2$, $x_2 = 2$, $y_2 = -4$:
$x = \frac{3(2) + 4(-2)}{3 + 4}$
$x = \frac{6 - 8}{7}$
$x = \frac{-2}{7}$
$y = \frac{3(-4) + 4(-2)}{3 + 4}$
$y = \frac{-12 - 8}{7}$
$y = \frac{-20}{7}$
Thus, the coordinates of point P are $(-\frac{2}{7}, -\frac{20}{7})$.
Therefore, the coordinates of P are $(-\frac{2}{7}, -\frac{20}{7})$.
Question 9. Find the coordinates of the points which divide the line segment joining A(– 2, 2) and B(2, 8) into four equal parts.
Answer:
Given
The line segment joining the points A(– 2, 2) and B(2, 8).
To Find
The coordinates of the points which divide the line segment AB into four equal parts.
Solution
Let the points which divide the line segment joining A(– 2, 2) and B(2, 8) into four equal parts be P, Q, and R.
This means that $AP = PQ = QR = RB$.
From the figure, it is clear that Q is the midpoint of the line segment AB.
P is the midpoint of the line segment AQ.
R is the midpoint of the line segment QB.
We will use the midpoint formula to find the coordinates of these points. The coordinates of the midpoint of a line segment joining points $(x_1, y_1)$ and $(x_2, y_2)$ is given by:
$M(x, y) = \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right)$
Coordinates of Q (Midpoint of AB)
The points are A(– 2, 2) and B(2, 8).
Coordinates of Q = $ \left( \frac{-2 + 2}{2}, \frac{2 + 8}{2} \right) $
Coordinates of Q = $ \left( \frac{0}{2}, \frac{10}{2} \right) $
Coordinates of Q = $ (0, 5) $
Coordinates of P (Midpoint of AQ)
The points are A(– 2, 2) and Q(0, 5).
Coordinates of P = $ \left( \frac{-2 + 0}{2}, \frac{2 + 5}{2} \right) $
Coordinates of P = $ \left( \frac{-2}{2}, \frac{7}{2} \right) $
Coordinates of P = $ \left( -1, \frac{7}{2} \right) $
Coordinates of R (Midpoint of QB)
The points are Q(0, 5) and B(2, 8).
Coordinates of R = $ \left( \frac{0 + 2}{2}, \frac{5 + 8}{2} \right) $
Coordinates of R = $ \left( \frac{2}{2}, \frac{13}{2} \right) $
Coordinates of R = $ \left( 1, \frac{13}{2} \right) $
Therefore, the coordinates of the points which divide the line segment joining A(– 2, 2) and B(2, 8) into four equal parts are $(-1, \frac{7}{2})$, $(0, 5)$, and $(1, \frac{13}{2})$.
Question 10. Find the area of a rhombus if its vertices are (3, 0), (4, 5), (– 1, 4) and (– 2, – 1) taken in Order .
[Hint: Area of a rhombus = $\frac{1}{2}$ (product of its diagonals)]
Answer:
Given:
Let the vertices of the rhombus, taken in order, be $A(3, 0)$, $B(4, 5)$, $C(-1, 4)$, and $D(-2, -1)$.
To Find:
The area of the rhombus ABCD.
Solution:
The diagonals of the rhombus are AC and BD.
We need to find the lengths of the diagonals using the distance formula: $d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$.
Length of diagonal AC:
Using points $A(3, 0)$ and $C(-1, 4)$:
$AC = \sqrt{(-1 - 3)^2 + (4 - 0)^2}$
$AC = \sqrt{(-4)^2 + (4)^2}$
$AC = \sqrt{16 + 16}$
$AC = \sqrt{32} = 4\sqrt{2}$ units.
Length of diagonal BD:
Using points $B(4, 5)$ and $D(-2, -1)$:
$BD = \sqrt{(-2 - 4)^2 + (-1 - 5)^2}$
$BD = \sqrt{(-6)^2 + (-6)^2}$
$BD = \sqrt{36 + 36}$
$BD = \sqrt{72} = 6\sqrt{2}$ units.
Now, we use the formula for the area of a rhombus:
Area of rhombus = $\frac{1}{2} \times (\text{product of diagonals})$
Area = $\frac{1}{2} \times AC \times BD$
Area = $\frac{1}{2} \times (4\sqrt{2}) \times (6\sqrt{2})$
Area = $\frac{1}{2} \times (4 \times 6) \times (\sqrt{2} \times \sqrt{2})$
Area = $\frac{1}{2} \times 24 \times 2$
Area = $\frac{1}{2} \times 48$
Area = 24 square units.
Therefore, the area of the rhombus is 24 square units.
Example 11 to 15 (Before Exercise 7.3)
Example 11. Find the area of a triangle whose vertices are (1, –1), (– 4, 6) and (–3, –5).
Answer:
Given:
The vertices of the triangle are $A(1, -1)$, $B(-4, 6)$, and $C(-3, -5)$.
To Find:
The area of the triangle ABC.
Solution:
Let the vertices be $(x_1, y_1) = (1, -1)$, $(x_2, y_2) = (-4, 6)$, and $(x_3, y_3) = (-3, -5)$.
The formula for the area of a triangle with given vertices is:
Area = $\frac{1}{2} |x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)|$
Substitute the coordinates of the vertices into the formula:
Area = $\frac{1}{2} |1(6 - (-5)) + (-4)(-5 - (-1)) + (-3)(-1 - 6)|$
Simplify the terms inside the absolute value:
Area = $\frac{1}{2} |1(6 + 5) + (-4)(-5 + 1) + (-3)(-7)|$
Area = $\frac{1}{2} |1(11) + (-4)(-4) + (-3)(-7)|$
Area = $\frac{1}{2} |11 + 16 + 21|$
Area = $\frac{1}{2} |48|$
Since the area must be positive, the absolute value of 48 is 48.
Area = $\frac{1}{2} \times 48$
Area = 24 square units.
Therefore, the area of the triangle is 24 square units.
Example 12. Find the area of a triangle formed by the points A(5, 2), B(4, 7) and C (7, – 4).
Answer:
Given:
The vertices of the triangle are $A(5, 2)$, $B(4, 7)$, and $C(7, -4)$.
To Find:
The area of the triangle ABC.
Solution:
Let the vertices be $(x_1, y_1) = (5, 2)$, $(x_2, y_2) = (4, 7)$, and $(x_3, y_3) = (7, -4)$.
The formula for the area of a triangle with given vertices $(x_1, y_1)$, $(x_2, y_2)$, and $(x_3, y_3)$ is:
$Area = \frac{1}{2} |x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)|$
Substitute the coordinates of the vertices A, B, and C into the formula:
$Area = \frac{1}{2} |5(7 - (-4)) + 4(-4 - 2) + 7(2 - 7)|$
Simplify the terms inside the absolute value:
$Area = \frac{1}{2} |5(7 + 4) + 4(-6) + 7(-5)|$
$Area = \frac{1}{2} |5(11) + (-24) + (-35)|$
$Area = \frac{1}{2} |55 - 24 - 35|$
$Area = \frac{1}{2} |55 - 59|$
$Area = \frac{1}{2} |-4|$
Since the area must be positive, the absolute value of -4 is 4.
$Area = \frac{1}{2} \times 4$
$Area = 2$ square units.
Therefore, the area of the triangle is 2 square units.
Example 13. Find the area of the triangle formed by the points P(–1.5, 3), Q(6, –2) and R(–3, 4).
Answer:
Given:
The vertices of the triangle are $P(-1.5, 3)$, $Q(6, -2)$, and $R(-3, 4)$.
To Find:
The area of the triangle PQR.
Solution:
Let the vertices be $(x_1, y_1) = (-1.5, 3)$, $(x_2, y_2) = (6, -2)$, and $(x_3, y_3) = (-3, 4)$.
The formula for the area of a triangle with given vertices $(x_1, y_1)$, $(x_2, y_2)$, and $(x_3, y_3)$ is:
$Area = \frac{1}{2} |x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)|$
Substitute the coordinates of the vertices P, Q, and R into the formula:
$Area = \frac{1}{2} |(-1.5)(-2 - 4) + (6)(4 - 3) + (-3)(3 - (-2))|$
Simplify the terms inside the absolute value:
$Area = \frac{1}{2} |(-1.5)(-6) + (6)(1) + (-3)(3 + 2)|$
$Area = \frac{1}{2} |(-1.5)(-6) + 6(1) + (-3)(5)|$
$Area = \frac{1}{2} |9 + 6 - 15|$
$Area = \frac{1}{2} |15 - 15|$
$Area = \frac{1}{2} |0|$
$Area = 0$ square units.
Since the area of the triangle is 0, the points P, Q, and R are collinear (they lie on the same straight line).
Therefore, the area of the triangle formed by the given points is 0 square units.
Example 14. Find the value of k if the points A(2, 3), B(4, k) and C(6, –3) are collinear.
Answer:
Given:
The points are $A(2, 3)$, $B(4, k)$, and $C(6, -3)$.
The points A, B, and C are collinear.
To Find:
The value of $k$.
Solution:
If three points $(x_1, y_1)$, $(x_2, y_2)$, and $(x_3, y_3)$ are collinear, then the area of the triangle formed by these points is zero.
The formula for the area of a triangle is:
$Area = \frac{1}{2} |x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)|$
For collinear points, Area = 0. This implies:
$x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) = 0$
Substitute the coordinates of A(2, 3), B(4, k), and C(6, -3) into the condition:
$(x_1, y_1) = (2, 3)$
$(x_2, y_2) = (4, k)$
$(x_3, y_3) = (6, -3)$
$2(k - (-3)) + 4(-3 - 3) + 6(3 - k) = 0$
Simplify the equation:
$2(k + 3) + 4(-6) + 6(3 - k) = 0$
$2k + 6 - 24 + 18 - 6k = 0$
Combine like terms:
$(2k - 6k) + (6 - 24 + 18) = 0$
$-4k + (24 - 24) = 0$
$-4k + 0 = 0$
$-4k = 0$
Divide by -4:
$k = \frac{0}{-4}$
$k = 0$
Therefore, the value of $k$ for which the points are collinear is 0.
Example 15. If A(–5, 7), B(– 4, –5), C(–1, –6) and D(4, 5) are the vertices of a quadrilateral, find the area of the quadrilateral ABCD.
Answer:
To Find:
The area of the quadrilateral ABCD.
Solution:
To find the area of the quadrilateral ABCD, we can divide it into two triangles by drawing one of the diagonals, for example, diagonal AC.
The area of the quadrilateral ABCD will be the sum of the areas of triangle ABC and triangle ADC.
The formula for the area of a triangle with vertices $(x_1, y_1)$, $(x_2, y_2)$, and $(x_3, y_3)$ is:
$Area = \frac{1}{2} |x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)|$
Area of Triangle ABC:
Vertices are $A(-5, 7)$, $B(-4, -5)$, $C(-1, -6)$.
$(x_1, y_1) = (-5, 7)$
$(x_2, y_2) = (-4, -5)$
$(x_3, y_3) = (-1, -6)$
$Area(\triangle ABC) = \frac{1}{2} |(-5)(-5 - (-6)) + (-4)(-6 - 7) \ $$ + (-1)(7 - (-5))|$
$Area(\triangle ABC) = \frac{1}{2} |(-5)(-5 + 6) + (-4)(-13) + (-1)(7 + 5)|$
$Area(\triangle ABC) = \frac{1}{2} |(-5)(1) + (52) + (-1)(12)|$
$Area(\triangle ABC) = \frac{1}{2} |-5 + 52 - 12|$
$Area(\triangle ABC) = \frac{1}{2} |52 - 17|$
$Area(\triangle ABC) = \frac{1}{2} |35| = \frac{35}{2}$ square units.
Area of Triangle ADC:
Vertices are $A(-5, 7)$, $D(4, 5)$, $C(-1, -6)$.
$(x_1, y_1) = (-5, 7)$
$(x_2, y_2) = (4, 5)$
$(x_3, y_3) = (-1, -6)$
$Area(\triangle ADC) = \frac{1}{2} |(-5)(5 - (-6)) + (4)(-6 - 7) + (-1)(7 - 5)|$
$Area(\triangle ADC) = \frac{1}{2} |(-5)(5 + 6) + (4)(-13) + (-1)(2)|$
$Area(\triangle ADC) = \frac{1}{2} |(-5)(11) + (-52) + (-2)|$
$Area(\triangle ADC) = \frac{1}{2} |-55 - 52 - 2|$
$Area(\triangle ADC) = \frac{1}{2} |-109|$
$Area(\triangle ADC) = \frac{109}{2}$ square units.
Area of Quadrilateral ABCD:
Area(ABCD) = Area($\triangle ABC$) + Area($\triangle ADC$)
Area(ABCD) = $\frac{35}{2} + \frac{109}{2}$
Area(ABCD) = $\frac{35 + 109}{2}$
Area(ABCD) = $\frac{144}{2}$
Area(ABCD) = 72 square units.
Therefore, the area of the quadrilateral ABCD is 72 square units.
Exercise 7.3
Question 1. Find the area of the triangle whose vertices are :
(i) (2, 3), (–1, 0), (2, – 4)
(ii) (–5, –1), (3, –5), (5, 2)
Answer:
The area of a triangle with vertices $(x_1, y_1)$, $(x_2, y_2)$, and $(x_3, y_3)$ is given by the formula:
$Area = \frac{1}{2} |x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)|$
(i)
Given vertices are $A(2, 3)$, $B(-1, 0)$, and $C(2, -4)$.
Let $(x_1, y_1) = (2, 3)$, $(x_2, y_2) = (-1, 0)$, and $(x_3, y_3) = (2, -4)$.
Substitute these coordinates into the area formula:
$Area = \frac{1}{2} |2(0 - (-4)) + (-1)(-4 - 3) + 2(3 - 0)|$
$Area = \frac{1}{2} |2(0 + 4) + (-1)(-7) + 2(3)|$
$Area = \frac{1}{2} |2(4) + 7 + 6|$
$Area = \frac{1}{2} |8 + 7 + 6|$
$Area = \frac{1}{2} |21|$
$Area = \frac{21}{2}$ square units.
The area of the triangle is $\frac{21}{2}$ or 10.5 square units.
(ii)
Given vertices are $P(-5, -1)$, $Q(3, -5)$, and $R(5, 2)$.
Let $(x_1, y_1) = (-5, -1)$, $(x_2, y_2) = (3, -5)$, and $(x_3, y_3) = (5, 2)$.
Substitute these coordinates into the area formula:
$Area = \frac{1}{2} |(-5)(-5 - 2) + (3)(2 - (-1)) + (5)(-1 - (-5))|$
$Area = \frac{1}{2} |(-5)(-7) + (3)(2 + 1) + (5)(-1 + 5)|$
$Area = \frac{1}{2} |35 + 3(3) + 5(4)|$
$Area = \frac{1}{2} |35 + 9 + 20|$
$Area = \frac{1}{2} |64|$
$Area = \frac{1}{2} \times 64$
$Area = 32$ square units.
The area of the triangle is 32 square units.
Question 2. In each of the following find the value of ‘k’, for which the points are collinear.
(i) (7, –2), (5, 1), (3, k)
(ii) (8, 1), (k, – 4), (2, –5)
Answer:
Concept:
For three points to be collinear, the area of the triangle formed by these points must be zero.
The area of a triangle with vertices $(x_1, y_1)$, $(x_2, y_2)$, and $(x_3, y_3)$ is given by:
$Area = \frac{1}{2} |x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)|$
Therefore, for collinear points, the condition is:
$x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) = 0$
(i)
Given:
The points are $A(7, -2)$, $B(5, 1)$, and $C(3, k)$. The points are collinear.
To Find:
The value of $k$.
Solution:
Let $(x_1, y_1) = (7, -2)$, $(x_2, y_2) = (5, 1)$, and $(x_3, y_3) = (3, k)$.
Applying the condition for collinearity:
$7(1 - k) + 5(k - (-2)) + 3(-2 - 1) = 0$
$7(1 - k) + 5(k + 2) + 3(-3) = 0$
$7 - 7k + 5k + 10 - 9 = 0$
Combine the terms involving $k$ and the constant terms:
$(-7k + 5k) + (7 + 10 - 9) = 0$
$-2k + (17 - 9) = 0$
$-2k + 8 = 0$
$-2k = -8$
$k = \frac{-8}{-2}$
$k = 4$
Therefore, the value of $k$ is 4.
(ii)
Given:
The points are $P(8, 1)$, $Q(k, -4)$, and $R(2, -5)$. The points are collinear.
To Find:
The value of $k$.
Solution:
Let $(x_1, y_1) = (8, 1)$, $(x_2, y_2) = (k, -4)$, and $(x_3, y_3) = (2, -5)$.
Applying the condition for collinearity:
$8(-4 - (-5)) + k(-5 - 1) + 2(1 - (-4)) = 0$
$8(-4 + 5) + k(-6) + 2(1 + 4) = 0$
$8(1) - 6k + 2(5) = 0$
$8 - 6k + 10 = 0$
Combine the constant terms:
$-6k + 18 = 0$
$-6k = -18$
$k = \frac{-18}{-6}$
$k = 3$
Therefore, the value of $k$ is 3.
Question 3. Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, –1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle.
Answer:
Given:
The vertices of the given triangle (let's call it $\triangle ABC$) are $A(0, -1)$, $B(2, 1)$, and $C(0, 3)$.
To Find:
1. The area of the triangle formed by joining the mid-points of the sides of $\triangle ABC$.
2. The ratio of the area of the smaller triangle (formed by midpoints) to the area of the given triangle ($\triangle ABC$).
Solution:
Step 1: Find the coordinates of the midpoints of the sides of $\triangle ABC$.
Let D, E, and F be the midpoints of the sides BC, AC, and AB, respectively.
We use the midpoint formula: $M = \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right)$.
Midpoint D of BC (B(2, 1), C(0, 3)):
$D = \left( \frac{2 + 0}{2}, \frac{1 + 3}{2} \right) = \left( \frac{2}{2}, \frac{4}{2} \right) = (1, 2)$
Midpoint E of AC (A(0, -1), C(0, 3)):
$E = \left( \frac{0 + 0}{2}, \frac{-1 + 3}{2} \right) = \left( \frac{0}{2}, \frac{2}{2} \right) = (0, 1)$
Midpoint F of AB (A(0, -1), B(2, 1)):
$F = \left( \frac{0 + 2}{2}, \frac{-1 + 1}{2} \right) = \left( \frac{2}{2}, \frac{0}{2} \right) = (1, 0)$
So, the vertices of the triangle formed by joining the midpoints ($\triangle DEF$) are D(1, 2), E(0, 1), and F(1, 0).
Step 2: Find the area of the triangle formed by the midpoints ($\triangle DEF$).
We use the area formula for a triangle with vertices $(x_1, y_1)$, $(x_2, y_2)$, and $(x_3, y_3)$:
$Area = \frac{1}{2} |x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)|$
For $\triangle DEF$ with D(1, 2), E(0, 1), F(1, 0):
$Area(\triangle DEF) = \frac{1}{2} |1(1 - 0) + 0(0 - 2) + 1(2 - 1)|$
$Area(\triangle DEF) = \frac{1}{2} |1(1) + 0(-2) + 1(1)|$
$Area(\triangle DEF) = \frac{1}{2} |1 + 0 + 1|$
$Area(\triangle DEF) = \frac{1}{2} |2| = 1$ square unit.
The area of the triangle formed by joining the mid-points is 1 square unit.
Step 3: Find the area of the given triangle ($\triangle ABC$).
Vertices are A(0, -1), B(2, 1), C(0, 3).
$Area(\triangle ABC) = \frac{1}{2} |0(1 - 3) + 2(3 - (-1)) + 0(-1 - 1)|$
$Area(\triangle ABC) = \frac{1}{2} |0(-2) + 2(3 + 1) + 0(-2)|$
$Area(\triangle ABC) = \frac{1}{2} |0 + 2(4) + 0|$
$Area(\triangle ABC) = \frac{1}{2} |8| = 4$ square units.
The area of the given triangle is 4 square units.
Step 4: Find the ratio of the areas.
Ratio = $\frac{Area(\triangle DEF)}{Area(\triangle ABC)}$
Ratio = $\frac{1}{4}$
The ratio of the area of the triangle formed by the mid-points to the area of the given triangle is 1 : 4.
Question 4. Find the area of the quadrilateral whose vertices, taken in order, are (– 4, – 2), (– 3, – 5), (3, – 2) and (2, 3).
Answer:
Given:
The vertices of the quadrilateral, taken in order, are $A(-4, -2)$, $B(-3, -5)$, $C(3, -2)$, and $D(2, 3)$.
To Find:
The area of the quadrilateral ABCD.
Solution:
To find the area of the quadrilateral ABCD, we can divide it into two triangles by joining the diagonal AC.
Area(Quadrilateral ABCD) = Area($\triangle ABC$) + Area($\triangle ADC$)
The area of a triangle with vertices $(x_1, y_1)$, $(x_2, y_2)$, and $(x_3, y_3)$ is given by:
$Area = \frac{1}{2} |x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)|$
Area of Triangle ABC:
Vertices are $A(-4, -2)$, $B(-3, -5)$, $C(3, -2)$.
Let $(x_1, y_1) = (-4, -2)$, $(x_2, y_2) = (-3, -5)$, $(x_3, y_3) = (3, -2)$.
$Area(\triangle ABC) = \frac{1}{2} |(-4)(-5 - (-2)) + (-3)(-2 - (-2)) \ $$ + (3)(-2 - (-5))|$
$Area(\triangle ABC) = \frac{1}{2} |(-4)(-5 + 2) + (-3)(-2 + 2) + (3)(-2 + 5)|$
$Area(\triangle ABC) = \frac{1}{2} |(-4)(-3) + (-3)(0) + (3)(3)|$
$Area(\triangle ABC) = \frac{1}{2} |12 + 0 + 9|$
$Area(\triangle ABC) = \frac{1}{2} |21| = \frac{21}{2}$ square units.
Area of Triangle ADC:
Vertices are $A(-4, -2)$, $D(2, 3)$, $C(3, -2)$.
Let $(x_1, y_1) = (-4, -2)$, $(x_2, y_2) = (2, 3)$, $(x_3, y_3) = (3, -2)$.
$Area(\triangle ADC) = \frac{1}{2} |(-4)(3 - (-2)) + (2)(-2 - (-2)) + (3)(-2 - 3)|$
$Area(\triangle ADC) = \frac{1}{2} |(-4)(3 + 2) + (2)(-2 + 2) + (3)(-5)|$
$Area(\triangle ADC) = \frac{1}{2} |(-4)(5) + (2)(0) + (3)(-5)|$
$Area(\triangle ADC) = \frac{1}{2} |-20 + 0 - 15|$
$Area(\triangle ADC) = \frac{1}{2} |-35| = \frac{35}{2}$ square units.
Area of Quadrilateral ABCD:
Area(ABCD) = Area($\triangle ABC$) + Area($\triangle ADC$)
Area(ABCD) = $\frac{21}{2} + \frac{35}{2}$
Area(ABCD) = $\frac{21 + 35}{2}$
Area(ABCD) = $\frac{56}{2}$
Area(ABCD) = 28 square units.
Therefore, the area of the quadrilateral ABCD is 28 square units.
Question 5. You have studied in Class IX, (Chapter 9, Example 3), that a median of a triangle divides it into two triangles of equal areas. Verify this result for ∆ ABC whose vertices are A(4, – 6), B(3, –2) and C(5, 2).
Answer:
Given:
The vertices of the triangle $\triangle ABC$ are $A(4, -6)$, $B(3, -2)$, and $C(5, 2)$.
We need to verify that a median divides the triangle into two triangles of equal areas.
To Verify:
If AD is a median of $\triangle ABC$, then Area($\triangle ABD$) = Area($\triangle ACD$).
Verification:
Let AD be the median from vertex A to the side BC. By definition, the median connects a vertex to the midpoint of the opposite side. So, D is the midpoint of BC.
Step 1: Find the coordinates of the midpoint D of BC.
Using the midpoint formula $M = \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right)$ for points $B(3, -2)$ and $C(5, 2)$.
$x_D = \frac{3 + 5}{2} = \frac{8}{2} = 4$
$y_D = \frac{-2 + 2}{2} = \frac{0}{2} = 0$
The coordinates of the midpoint D are (4, 0).
Step 2: Calculate the area of $\triangle ABD$.
The vertices of $\triangle ABD$ are $A(4, -6)$, $B(3, -2)$, and $D(4, 0)$.
Using the area formula $Area = \frac{1}{2} |x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)|$:
$Area(\triangle ABD) = \frac{1}{2} |4(-2 - 0) + 3(0 - (-6)) + 4(-6 - (-2))|$
$Area(\triangle ABD) = \frac{1}{2} |4(-2) + 3(6) + 4(-6 + 2)|$
$Area(\triangle ABD) = \frac{1}{2} |-8 + 18 + 4(-4)|$
$Area(\triangle ABD) = \frac{1}{2} |-8 + 18 - 16|$
$Area(\triangle ABD) = \frac{1}{2} |18 - 24|$
$Area(\triangle ABD) = \frac{1}{2} |-6| = \frac{1}{2} \times 6 = 3$ square units.
Step 3: Calculate the area of $\triangle ACD$.
The vertices of $\triangle ACD$ are $A(4, -6)$, $C(5, 2)$, and $D(4, 0)$.
Using the area formula:
$Area(\triangle ACD) = \frac{1}{2} |4(2 - 0) + 5(0 - (-6)) + 4(-6 - 2)|$
$Area(\triangle ACD) = \frac{1}{2} |4(2) + 5(6) + 4(-8)|$
$Area(\triangle ACD) = \frac{1}{2} |8 + 30 - 32|$
$Area(\triangle ACD) = \frac{1}{2} |38 - 32|$
$Area(\triangle ACD) = \frac{1}{2} |6| = \frac{1}{2} \times 6 = 3$ square units.
Step 4: Compare the areas.
We found that Area($\triangle ABD$) = 3 square units and Area($\triangle ACD$) = 3 square units.
Since Area($\triangle ABD$) = Area($\triangle ACD$), the median AD divides $\triangle ABC$ into two triangles of equal areas.
This verifies the result for the given $\triangle ABC$.
Exercise 7.4 (Optional)
Question 1. Determine the ratio in which the line 2x + y – 4 = 0 divides the line segment joining the points A(2, – 2) and B(3, 7).
Answer:
Given:
The line segment joins the points $A(2, -2)$ and $B(3, 7)$.
The line is given by the equation $2x + y - 4 = 0$.
To Find:
The ratio in which the line $2x + y - 4 = 0$ divides the line segment joining A and B.
Solution:
Let the line $2x + y - 4 = 0$ intersect the line segment joining $A(x_1, y_1) = (2, -2)$ and $B(x_2, y_2) = (3, 7)$ at point $P(x, y)$.
Let the ratio in which P divides AB be $m_1 : m_2$.
Assume the ratio is $k : 1$. Then $m_1 = k$ and $m_2 = 1$.
Using the section formula, the coordinates of the point P are:
$x = \frac{m_1 x_2 + m_2 x_1}{m_1 + m_2} = \frac{k(3) + 1(2)}{k + 1} = \frac{3k + 2}{k + 1}$
$y = \frac{m_1 y_2 + m_2 y_1}{m_1 + m_2} = \frac{k(7) + 1(-2)}{k + 1} = \frac{7k - 2}{k + 1}$
So, the coordinates of the point P are $\left( \frac{3k + 2}{k + 1}, \frac{7k - 2}{k + 1} \right)$.
Since the point P lies on the line $2x + y - 4 = 0$, its coordinates must satisfy the equation of the line.
Substitute the coordinates of P into the equation of the line:
$2\left( \frac{3k + 2}{k + 1} \right) + \left( \frac{7k - 2}{k + 1} \right) - 4 = 0$
Multiply the entire equation by $(k + 1)$ to eliminate the denominator:
$2(3k + 2) + (7k - 2) - 4(k + 1) = 0$
$6k + 4 + 7k - 2 - 4k - 4 = 0$
Combine the terms with $k$ and the constant terms:
$(6k + 7k - 4k) + (4 - 2 - 4) = 0$
$9k - 2 = 0$
$9k = 2$
$k = \frac{2}{9}$
The ratio $k : 1$ is $\frac{2}{9} : 1$.
Multiplying by 9, we get the ratio $2 : 9$.
Since $k = 2/9$ is positive, the division is internal.
Therefore, the line $2x + y - 4 = 0$ divides the line segment joining the points A(2, – 2) and B(3, 7) in the ratio 2 : 9.
Alternate Solution:
The ratio in which the line $ax + by + c = 0$ divides the line segment joining points $(x_1, y_1)$ and $(x_2, y_2)$ is given by the formula:
$Ratio = -\frac{ax_1 + by_1 + c}{ax_2 + by_2 + c}$
Here, the line is $2x + y - 4 = 0$, so $a=2, b=1, c=-4$.
The points are $A(x_1, y_1) = (2, -2)$ and $B(x_2, y_2) = (3, 7)$.
Calculate the value of the expression $ax + by + c$ for point A:
$2(2) + 1(-2) - 4 = 4 - 2 - 4 = -2$
Calculate the value of the expression $ax + by + c$ for point B:
$2(3) + 1(7) - 4 = 6 + 7 - 4 = 13 - 4 = 9$
Substitute these values into the ratio formula:
$Ratio = -\frac{(-2)}{(9)} = \frac{2}{9}$
The ratio is $2 : 9$.
Since the ratio is positive, the division is internal.
Thus, the required ratio is 2 : 9.
Question 2. Find a relation between x and y if the points (x, y), (1, 2) and (7, 0) are collinear.
Answer:
Given:
The points $A(x, y)$, $B(1, 2)$, and $C(7, 0)$ are collinear.
To Find:
A relation between $x$ and $y$.
Solution:
If three points are collinear, the area of the triangle formed by these points is zero.
The area of a triangle with vertices $(x_1, y_1)$, $(x_2, y_2)$, and $(x_3, y_3)$ is given by:
$Area = \frac{1}{2} |x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)|$
For collinear points, Area = 0. Therefore, the condition for collinearity is:
$x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) = 0$
Let the points be $(x_1, y_1) = (x, y)$, $(x_2, y_2) = (1, 2)$, and $(x_3, y_3) = (7, 0)$.
Substitute these coordinates into the collinearity condition:
$x(2 - 0) + 1(0 - y) + 7(y - 2) = 0$
Simplify the equation:
$x(2) + 1(-y) + 7(y - 2) = 0$
$2x - y + 7y - 14 = 0$
Combine like terms:
$2x + (-y + 7y) - 14 = 0$
$2x + 6y - 14 = 0$
Divide the entire equation by 2 to simplify:
$\frac{2x}{2} + \frac{6y}{2} - \frac{14}{2} = \frac{0}{2}$
$x + 3y - 7 = 0$
This can also be written as $x + 3y = 7$.
Therefore, the required relation between $x$ and $y$ is $x + 3y = 7$.
Alternate Solution (Using Slope):
If points A(x, y), B(1, 2), and C(7, 0) are collinear, then the slope of AB must be equal to the slope of BC.
Slope of AB = $\frac{2 - y}{1 - x}$
Slope of BC = $\frac{0 - 2}{7 - 1} = \frac{-2}{6} = -\frac{1}{3}$
Equating the slopes:
$\frac{2 - y}{1 - x} = -\frac{1}{3}$
Cross-multiply:
$3(2 - y) = -1(1 - x)$
$6 - 3y = -1 + x$
Rearrange the terms:
$6 + 1 = x + 3y$
$7 = x + 3y$
The relation is $x + 3y = 7$.
Question 3. Find the centre of a circle passing through the points (6, – 6), (3, – 7) and (3, 3).
Answer:
Given:
A circle passes through the points $A(6, -6)$, $B(3, -7)$, and $C(3, 3)$.
To Find:
The coordinates of the centre of the circle.
Solution:
Let the centre of the circle be $O(x, y)$.
Since the points A, B, and C lie on the circle, the distance from the centre O to each of these points is equal (equal to the radius).
Therefore, $OA = OB = OC$.
This implies that the squares of the distances are also equal: $OA^2 = OB^2 = OC^2$.
We use the distance formula squared: $d^2 = (x_2 - x_1)^2 + (y_2 - y_1)^2$.
Calculating the squared distances:
$OA^2 = (x - 6)^2 + (y - (-6))^2 = (x - 6)^2 + (y + 6)^2$
$OA^2 = (x^2 - 12x + 36) + (y^2 + 12y + 36) = x^2 + y^2 - 12x + 12y \ $$ + 72$
$OB^2 = (x - 3)^2 + (y - (-7))^2 = (x - 3)^2 + (y + 7)^2$
$OB^2 = (x^2 - 6x + 9) + (y^2 + 14y + 49) = x^2 + y^2 - 6x + 14y + 58$
$OC^2 = (x - 3)^2 + (y - 3)^2$
$OC^2 = (x^2 - 6x + 9) + (y^2 - 6y + 9) = x^2 + y^2 - 6x - 6y + 18$
Now, we set up equations using the equalities.
Equating $OA^2$ and $OB^2$:
$OA^2 = OB^2$
$x^2 + y^2 - 12x + 12y + 72 = x^2 + y^2 - 6x + 14y + 58$
Cancel $x^2$ and $y^2$ terms:
$-12x + 12y + 72 = -6x + 14y + 58$
Rearrange terms to form a linear equation in $x$ and $y$:
$72 - 58 = -6x + 12x + 14y - 12y$
$14 = 6x + 2y$
Divide the equation by 2:
$3x + y = 7$
...(i)
Equating $OB^2$ and $OC^2$:
$OB^2 = OC^2$
$x^2 + y^2 - 6x + 14y + 58 = x^2 + y^2 - 6x - 6y + 18$
Cancel $x^2$, $y^2$, and $-6x$ terms:
$14y + 58 = -6y + 18$
Rearrange terms to solve for $y$:
$14y + 6y = 18 - 58$
$20y = -40$
$y = \frac{-40}{20}$
$y = -2$
Finding the value of x:
Substitute the value $y = -2$ into equation (i):
$3x + (-2) = 7$
$3x - 2 = 7$
$3x = 7 + 2$
$3x = 9$
$x = \frac{9}{3}$
$x = 3$
Thus, the coordinates of the centre $O(x, y)$ are $(3, -2)$.
Therefore, the centre of the circle passing through the given points is (3, –2).
Question 4. The two opposite vertices of a square are (–1, 2) and (3, 2). Find the coordinates of the other two vertices.
Answer:
Given
The two opposite vertices of a square are (–1, 2) and (3, 2).
To Find
The coordinates of the other two vertices of the square.
Solution
Let the given opposite vertices of the square be A(–1, 2) and C(3, 2). Let the other two vertices be B$(x, y)$ and D$(x_1, y_1)$.
We know that the diagonals of a square have the following properties:
1. They bisect each other (i.e., they share the same midpoint).
2. They are equal in length.
3. They are perpendicular to each other.
First, let's find the midpoint of the diagonal AC. Let this midpoint be O.
Using the midpoint formula, $O = \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right)$:
Coordinates of O = $ \left( \frac{-1 + 3}{2}, \frac{2 + 2}{2} \right) = \left( \frac{2}{2}, \frac{4}{2} \right) = (1, 2) $
Since the diagonals bisect each other, O(1, 2) is also the midpoint of the diagonal BD.
Now, let's use the property that in a square, all sides are equal. Let the coordinates of vertex B be $(x, y)$.
In the square ABCD, AB = BC.
Therefore, $AB^2 = BC^2$.
Using the distance formula, $d^2 = (x_2 - x_1)^2 + (y_2 - y_1)^2$:
$ (x - (-1))^2 + (y - 2)^2 = (x - 3)^2 + (y - 2)^2 $
$ (x + 1)^2 + (y - 2)^2 = (x - 3)^2 + (y - 2)^2 $
Cancelling $(y - 2)^2$ from both sides:
$ (x + 1)^2 = (x - 3)^2 $
$ x^2 + 2x + 1 = x^2 - 6x + 9 $
$ 2x + 1 = -6x + 9 $
$ 8x = 8 $
$ x = 1 $
Now consider the triangle $\triangle ABC$. Since ABCD is a square, $\angle B = 90^\circ$. Therefore, $\triangle ABC$ is a right-angled triangle.
By the Pythagorean theorem, $AB^2 + BC^2 = AC^2$.
First, let's calculate the length of the diagonal AC squared:
$ AC^2 = (3 - (-1))^2 + (2 - 2)^2 = (4)^2 + (0)^2 = 16 $
Now, substitute $x = 1$ into the expressions for $AB^2$ and $BC^2$:
$ AB^2 = (1 + 1)^2 + (y - 2)^2 = 2^2 + (y - 2)^2 = 4 + (y - 2)^2 $
$ BC^2 = (1 - 3)^2 + (y - 2)^2 = (-2)^2 + (y - 2)^2 = 4 + (y - 2)^2 $
Now, apply the Pythagorean theorem:
$ (4 + (y - 2)^2) + (4 + (y - 2)^2) = 16 $
$ 8 + 2(y - 2)^2 = 16 $
$ 2(y - 2)^2 = 16 - 8 $
$ 2(y - 2)^2 = 8 $
$ (y - 2)^2 = 4 $
Taking the square root on both sides:
$ y - 2 = \pm 2 $
This gives us two possible values for y:
$ y - 2 = 2 \implies y = 4 $
$ y - 2 = -2 \implies y = 0 $
So, the coordinates of the other two vertices are (1, 4) and (1, 0).
Hence, the coordinates of the other two vertices of the square are (1, 4) and (1, 0).
Question 5. The Class X students of a secondary school in Krishinagar have been allotted a rectangular plot of land for their gardening activity. Sapling of Gulmohar are planted on the boundary at a distance of 1m from each other. There is a triangular grassy lawn in the plot as shown in the Fig. 7.14. The students are to sow seeds of flowering plants on the remaining area of the plot.
(i) Taking A as origin, find the coordinates of the vertices of the triangle.
(ii) What will be the coordinates of the vertices of ∆ PQR if C is the origin? Also calculate the areas of the triangles in these cases. What do you observe?
Answer:
First, we need to determine the coordinates of the vertices of the rectangle and the triangle from the given figure.
(i) Taking A as origin, find the coordinates of the vertices of the triangle.
If we take A as the origin (0, 0), AD as the x-axis, and AB as the y-axis, we can find the coordinates of the vertices P, Q, and R by observing their positions.
- The coordinates of P are found by moving 4 units along the x-axis and 6 units along the y-axis. So, P = (4, 6).
- The coordinates of Q are found by moving 3 units along the x-axis and 2 units along the y-axis. So, Q = (3, 2).
- The coordinates of R are found by moving 6 units along the x-axis and 5 units along the y-axis. So, R = (6, 5).
Thus, with A as the origin, the coordinates of the vertices of the triangle are P(4, 6), Q(3, 2), and R(6, 5).
(ii) What will be the coordinates of the vertices of ∆ PQR if C is the origin? Also calculate the areas of the triangles in these cases. What do you observe?
Coordinates with C as the origin:
To find the coordinates with C as the origin, we first need to determine the coordinates of the vertex C when A is the origin. By counting the saplings along the boundary (assuming each is 1m apart), we find that the length AD/BC is 16m and the width AB/CD is 8m. Therefore, with A as the origin (0,0), the coordinates of C are (16, 8).
Now, if C is the origin (0, 0), then CB is the new x-axis and CD is the new y-axis.
The new coordinates $(x', y')$ of a point $(x, y)$ can be found by calculating its perpendicular distance from the new axes CD and CB.
$x' = \text{distance from CD} = \text{Total length} - x = 16 - x$
$y' = \text{distance from CB} = \text{Total width} - y = 8 - y$
Using this transformation for vertices P, Q, and R:
- For vertex P(4, 6): New coordinates are $(16-4, 8-6) = (12, 2)$.
- For vertex Q(3, 2): New coordinates are $(16-3, 8-2) = (13, 6)$.
- For vertex R(6, 5): New coordinates are $(16-6, 8-5) = (10, 3)$.
Thus, with C as the origin, the coordinates of the vertices of the triangle are P(12, 2), Q(13, 6), and R(10, 3).
Calculation of Areas:
The area of a triangle with vertices $(x_1, y_1)$, $(x_2, y_2)$, and $(x_3, y_3)$ is given by:
Area = $\frac{1}{2} |x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)|$
Case 1: A as origin
Vertices are P(4, 6), Q(3, 2), and R(6, 5).
Area of $\triangle PQR = \frac{1}{2} |4(2 - 5) + 3(5 - 6) + 6(6 - 2)|$
Area of $\triangle PQR = \frac{1}{2} |4(-3) + 3(-1) + 6(4)|$
Area of $\triangle PQR = \frac{1}{2} |-12 - 3 + 24|$
Area of $\triangle PQR = \frac{1}{2} |9| = \frac{9}{2}$ square units.
Case 2: C as origin
Vertices are P(12, 2), Q(13, 6), and R(10, 3).
Area of $\triangle PQR = \frac{1}{2} |12(6 - 3) + 13(3 - 2) + 10(2 - 6)|$
Area of $\triangle PQR = \frac{1}{2} |12(3) + 13(1) + 10(-4)|$
Area of $\triangle PQR = \frac{1}{2} |36 + 13 - 40|$
Area of $\triangle PQR = \frac{1}{2} |49 - 40| = \frac{1}{2} |9| = \frac{9}{2}$ square units.
Observation:
The area of the triangle is $\frac{9}{2}$ square units in both cases. We observe that the area of the triangle remains the same even when the origin is changed. This is because a change in the coordinate system's origin only shifts the position of the figure without altering its size or shape.
Question 6. The vertices of a ∆ABC are A(4, 6), B(1, 5) and C(7, 2). A line is drawn to intersect sides AB and AC at D and E respectively, such that $\frac{AD}{AB}$ = $\frac{AE}{AC}$ = $\frac{1}{4}$ . Calculate the area of the ∆ ADE and compare it with the area of ∆ABC. (Recall Theorem 6.2 and Theorem 6.6).
Answer:
Given
The vertices of a ∆ABC are A(4, 6), B(1, 5) and C(7, 2).
A line intersects sides AB and AC at D and E respectively, such that:
$\frac{AD}{AB} = \frac{AE}{AC} = \frac{1}{4}$
To Find
Calculate the area of the ∆ ADE and compare it with the area of ∆ABC.
Solution
First, we need to find the coordinates of the points D and E.
Finding coordinates of D:
Point D lies on the side AB. We are given $\frac{AD}{AB} = \frac{1}{4}$.
This implies that D divides the line segment AB in the ratio 1:3 (since AD is 1 part and AB is 4 parts, DB must be $4-1=3$ parts).
So, D divides AB in the ratio $m_1:m_2 = 1:3$.
Using the section formula for a point $(x, y)$ dividing a line segment joining $(x_1, y_1)$ and $(x_2, y_2)$ in the ratio $m_1:m_2$:
$(x, y) = \left( \frac{m_1x_2 + m_2x_1}{m_1 + m_2}, \frac{m_1y_2 + m_2y_1}{m_1 + m_2} \right)$
Here, A(4, 6) is $(x_1, y_1)$ and B(1, 5) is $(x_2, y_2)$.
Coordinates of D = $ \left( \frac{1(1) + 3(4)}{1 + 3}, \frac{1(5) + 3(6)}{1 + 3} \right) $
Coordinates of D = $ \left( \frac{1 + 12}{4}, \frac{5 + 18}{4} \right) = \left( \frac{13}{4}, \frac{23}{4} \right) $
Finding coordinates of E:
Point E lies on the side AC. We are given $\frac{AE}{AC} = \frac{1}{4}$.
This implies that E divides the line segment AC in the ratio 1:3.
So, E divides AC in the ratio $m_1:m_2 = 1:3$.
Here, A(4, 6) is $(x_1, y_1)$ and C(7, 2) is $(x_2, y_2)$.
Coordinates of E = $ \left( \frac{1(7) + 3(4)}{1 + 3}, \frac{1(2) + 3(6)}{1 + 3} \right) $
Coordinates of E = $ \left( \frac{7 + 12}{4}, \frac{2 + 18}{4} \right) = \left( \frac{19}{4}, \frac{20}{4} \right) = \left( \frac{19}{4}, 5 \right) $
Calculating the area of ∆ ADE:
The vertices of ∆ ADE are A(4, 6), D($\frac{13}{4}, \frac{23}{4}$), and E($\frac{19}{4}, 5$).
Using the area formula for a triangle with vertices $(x_1, y_1)$, $(x_2, y_2)$, and $(x_3, y_3)$:
Area = $\frac{1}{2} |x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)|$
Area(∆ ADE) = $ \frac{1}{2} \left| 4(\frac{23}{4} - 5) + \frac{13}{4}(5 - 6) + \frac{19}{4}(6 - \frac{23}{4}) \right| $
Area(∆ ADE) = $ \frac{1}{2} \left| 4(\frac{23 - 20}{4}) + \frac{13}{4}(-1) + \frac{19}{4}(\frac{24 - 23}{4}) \right| $
Area(∆ ADE) = $ \frac{1}{2} \left| 4(\frac{3}{4}) - \frac{13}{4} + \frac{19}{16} \right| $
Area(∆ ADE) = $ \frac{1}{2} \left| 3 - \frac{13}{4} + \frac{19}{16} \right| $
Area(∆ ADE) = $ \frac{1}{2} \left| \frac{48 - 52 + 19}{16} \right| = \frac{1}{2} \left| \frac{15}{16} \right| = \frac{15}{32} $ square units.
Calculating the area of ∆ ABC:
The vertices of ∆ ABC are A(4, 6), B(1, 5), and C(7, 2).
Area(∆ ABC) = $ \frac{1}{2} |4(5 - 2) + 1(2 - 6) + 7(6 - 5)| $
Area(∆ ABC) = $ \frac{1}{2} |4(3) + 1(-4) + 7(1)| $
Area(∆ ABC) = $ \frac{1}{2} |12 - 4 + 7| = \frac{1}{2} |15| = \frac{15}{2} $ square units.
Comparison of Areas:
To compare the areas, we find their ratio:
$ \frac{\text{Area(∆ ADE)}}{\text{Area(∆ ABC)}} = \frac{15/32}{15/2} = \frac{15}{32} \times \frac{2}{15} = \frac{\cancel{15} \times \cancel{2}^1}{\cancel{32}_{16} \times \cancel{15}} = \frac{1}{16} $
Therefore, Area(∆ ADE) = $\frac{1}{16}$ Area(∆ ABC).
Recall Theorem 6.2 and Theorem 6.6:
The given condition is $\frac{AD}{AB} = \frac{AE}{AC} = \frac{1}{4}$. This means D and E divide the sides AB and AC in the same ratio. By the Converse of Basic Proportionality Theorem (Theorem 6.2), the line segment DE is parallel to BC (DE || BC).
Since DE || BC, ∆ ADE is similar to ∆ ABC (∆ ADE ~ ∆ ABC).
Theorem 6.6 states that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
$ \frac{\text{Area(∆ ADE)}}{\text{Area(∆ ABC)}} = \left(\frac{AD}{AB}\right)^2 $
$ \frac{\text{Area(∆ ADE)}}{\text{Area(∆ ABC)}} = \left(\frac{1}{4}\right)^2 = \frac{1}{16} $
This confirms our result obtained using coordinate geometry.
Question 7. Let A (4, 2), B(6, 5) and C(1, 4) be the vertices of ∆ABC.
(i) The median from A meets BC at D. Find the coordinates of the point D.
(ii) Find the coordinates of the point P on AD such that AP : PD = 2 : 1
(iii) Find the coordinates of points Q and R on medians BE and CF respectively such that BQ : QE = 2 : 1 and CR : RF = 2 : 1.
(iv) What do yo observe?
[Note: The point which is common to all the three medians is called the centroid and this point divides each median in the ratio 2 : 1.]
(v) If A(x1 , y1 ), B(x2 , y2 ) and C(x3 , y3 ) are the vertices of ∆ABC, find the coordinates of the centroid of the triangle.
Answer:
Given
The vertices of a ∆ABC are A(4, 2), B(6, 5), and C(1, 4).
(i) The median from A meets BC at D. Find the coordinates of the point D.
Solution
The median from vertex A meets the opposite side BC at its midpoint, D.
We use the midpoint formula to find the coordinates of D, which is the midpoint of B(6, 5) and C(1, 4).
Midpoint $(x, y) = \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right)$
Coordinates of D = $ \left( \frac{6 + 1}{2}, \frac{5 + 4}{2} \right) $
Coordinates of D = $ \left( \frac{7}{2}, \frac{9}{2} \right) $
Thus, the coordinates of point D are ($\frac{7}{2}, \frac{9}{2}$).
(ii) Find the coordinates of the point P on AD such that AP : PD = 2 : 1.
Solution
Point P divides the line segment AD in the ratio 2:1. We use the section formula.
The vertices are A(4, 2) and D($\frac{7}{2}, \frac{9}{2}$). The ratio is $m_1:m_2 = 2:1$.
Section Formula $(x, y) = \left( \frac{m_1x_2 + m_2x_1}{m_1 + m_2}, \frac{m_1y_2 + m_2y_1}{m_1 + m_2} \right)$
Coordinates of P = $ \left( \frac{2(\frac{7}{2}) + 1(4)}{2 + 1}, \frac{2(\frac{9}{2}) + 1(2)}{2 + 1} \right) $
Coordinates of P = $ \left( \frac{7 + 4}{3}, \frac{9 + 2}{3} \right) = \left( \frac{11}{3}, \frac{11}{3} \right) $
Thus, the coordinates of point P are ($\frac{11}{3}, \frac{11}{3}$).
(iii) Find the coordinates of points Q and R on medians BE and CF respectively such that BQ : QE = 2 : 1 and CR : RF = 2 : 1.
Solution
First, we find the coordinates of the midpoints E (on AC) and F (on AB).
Coordinates of E (midpoint of AC):
A(4, 2) and C(1, 4)
Coordinates of E = $ \left( \frac{4 + 1}{2}, \frac{2 + 4}{2} \right) = \left( \frac{5}{2}, \frac{6}{2} \right) = \left( \frac{5}{2}, 3 \right) $
Coordinates of Q (divides BE in ratio 2:1):
B(6, 5) and E($\frac{5}{2}, 3$)
Coordinates of Q = $ \left( \frac{2(\frac{5}{2}) + 1(6)}{2 + 1}, \frac{2(3) + 1(5)}{2 + 1} \right) = \left( \frac{5 + 6}{3}, \frac{6 + 5}{3} \right) = \left( \frac{11}{3}, \frac{11}{3} \right) $
Coordinates of F (midpoint of AB):
A(4, 2) and B(6, 5)
Coordinates of F = $ \left( \frac{4 + 6}{2}, \frac{2 + 5}{2} \right) = \left( \frac{10}{2}, \frac{7}{2} \right) = \left( 5, \frac{7}{2} \right) $
Coordinates of R (divides CF in ratio 2:1):
C(1, 4) and F($5, \frac{7}{2}$)
Coordinates of R = $ \left( \frac{2(5) + 1(1)}{2 + 1}, \frac{2(\frac{7}{2}) + 1(4)}{2 + 1} \right) = \left( \frac{10 + 1}{3}, \frac{7 + 4}{3} \right) = \left( \frac{11}{3}, \frac{11}{3} \right) $
Thus, the coordinates of Q and R are both ($\frac{11}{3}, \frac{11}{3}$).
(iv) What do you observe?
Observation
We observe that the coordinates of the points P, Q, and R are the same, i.e., P = Q = R = ($\frac{11}{3}, \frac{11}{3}$).
This means that the medians of the triangle are concurrent (they intersect at a single point). This point of concurrency, which divides each median in the ratio 2:1, is called the centroid of the triangle.
(v) If A(x1 , y1 ), B(x2 , y2 ) and C(x3 , y3 ) are the vertices of ∆ABC, find the coordinates of the centroid of the triangle.
Solution
Let the vertices of the triangle be A($x_1, y_1$), B($x_2, y_2$), and C($x_3, y_3$).
Let AD be the median from vertex A to the side BC. The coordinates of the midpoint D of BC are:
D = $ \left( \frac{x_2 + x_3}{2}, \frac{y_2 + y_3}{2} \right) $
The centroid of the triangle, let's call it G, divides the median AD in the ratio 2:1. Using the section formula with vertices A($x_1, y_1$) and D($\frac{x_2 + x_3}{2}, \frac{y_2 + y_3}{2}$) and ratio $m_1:m_2 = 2:1$:
Coordinates of G(x, y) = $ \left( \frac{2(\frac{x_2 + x_3}{2}) + 1(x_1)}{2 + 1}, \frac{2(\frac{y_2 + y_3}{2}) + 1(y_1)}{2 + 1} \right) $
The x-coordinate is: $ x = \frac{x_2 + x_3 + x_1}{3} = \frac{x_1 + x_2 + x_3}{3} $
The y-coordinate is: $ y = \frac{y_2 + y_3 + y_1}{3} = \frac{y_1 + y_2 + y_3}{3} $
Therefore, the coordinates of the centroid of a triangle with vertices A($x_1, y_1$), B($x_2, y_2$), and C($x_3, y_3$) are given by the formula:
Centroid G = $ \left( \frac{x_1 + x_2 + x_3}{3}, \frac{y_1 + y_2 + y_3}{3} \right) $
Question 8. ABCD is a rectangle formed by the points A(–1, –1), B(–1, 4), C(5, 4) and D(5, –1). P, Q, R and S are the mid-points of AB, BC, CD and DA respectively. Is the quadrilateral PQRS a square? a rectangle? or a rhombus? Justify your answer.
Answer:
Given
A rectangle ABCD with vertices A(–1, –1), B(–1, 4), C(5, 4) and D(5, –1).
P, Q, R, and S are the mid-points of the sides AB, BC, CD, and DA respectively.
To Find
Determine whether the quadrilateral PQRS is a square, a rectangle, or a rhombus, and justify the answer.
Solution
First, we need to find the coordinates of the points P, Q, R, and S using the midpoint formula.
The midpoint of a line segment joining points $(x_1, y_1)$ and $(x_2, y_2)$ is given by:
$M(x, y) = \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right)$
Coordinates of P (midpoint of AB):
A(–1, –1) and B(–1, 4)
P = $ \left( \frac{-1 + (-1)}{2}, \frac{-1 + 4}{2} \right) = \left( \frac{-2}{2}, \frac{3}{2} \right) = (-1, \frac{3}{2}) $
Coordinates of Q (midpoint of BC):
B(–1, 4) and C(5, 4)
Q = $ \left( \frac{-1 + 5}{2}, \frac{4 + 4}{2} \right) = \left( \frac{4}{2}, \frac{8}{2} \right) = (2, 4) $
Coordinates of R (midpoint of CD):
C(5, 4) and D(5, –1)
R = $ \left( \frac{5 + 5}{2}, \frac{4 + (-1)}{2} \right) = \left( \frac{10}{2}, \frac{3}{2} \right) = (5, \frac{3}{2}) $
Coordinates of S (midpoint of DA):
D(5, –1) and A(–1, –1)
S = $ \left( \frac{5 + (-1)}{2}, \frac{-1 + (-1)}{2} \right) = \left( \frac{4}{2}, \frac{-2}{2} \right) = (2, -1) $
Now, we find the lengths of the sides of the quadrilateral PQRS using the distance formula:
$d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$
Length of PQ:
$PQ = \sqrt{(2 - (-1))^2 + (4 - \frac{3}{2})^2} = \sqrt{(3)^2 + (\frac{8-3}{2})^2} = \sqrt{9 + (\frac{5}{2})^2} \ $$ = \sqrt{9 + \frac{25}{4}} = \sqrt{\frac{36+25}{4}} = \sqrt{\frac{61}{4}}$
Length of QR:
$QR = \sqrt{(5 - 2)^2 + (\frac{3}{2} - 4)^2} = \sqrt{(3)^2 + (\frac{3-8}{2})^2} = \sqrt{9 + (\frac{-5}{2})^2} \ $$ = \sqrt{9 + \frac{25}{4}} = \sqrt{\frac{36+25}{4}} = \sqrt{\frac{61}{4}}$
Length of RS:
$RS = \sqrt{(2 - 5)^2 + (-1 - \frac{3}{2})^2} = \sqrt{(-3)^2 + (\frac{-2-3}{2})^2} = \sqrt{9 + (\frac{-5}{2})^2} \ $$ = \sqrt{9 + \frac{25}{4}} = \sqrt{\frac{36+25}{4}} = \sqrt{\frac{61}{4}}$
Length of SP:
$SP = \sqrt{(-1 - 2)^2 + (\frac{3}{2} - (-1))^2} = \sqrt{(-3)^2 + (\frac{3+2}{2})^2} = \sqrt{9 + (\frac{5}{2})^2} \ $$ = \sqrt{9 + \frac{25}{4}} = \sqrt{\frac{36+25}{4}} = \sqrt{\frac{61}{4}}$
Since all four sides are equal ($PQ = QR = RS = SP$), the quadrilateral PQRS is either a rhombus or a square.
To determine if it is a square, we must check if the diagonals are equal.
Length of diagonal PR:
$PR = \sqrt{(5 - (-1))^2 + (\frac{3}{2} - \frac{3}{2})^2} = \sqrt{(6)^2 + (0)^2} = \sqrt{36} = 6$
Length of diagonal QS:
$QS = \sqrt{(2 - 2)^2 + (-1 - 4)^2} = \sqrt{(0)^2 + (-5)^2} = \sqrt{25} = 5$
Here, the lengths of the diagonals are not equal ($PR \neq QS$).
Justification
The quadrilateral PQRS has all four sides of equal length ($\sqrt{\frac{61}{4}}$ units), but its diagonals are of unequal lengths (6 units and 5 units). A quadrilateral with all sides equal and unequal diagonals is a rhombus.
Therefore, the quadrilateral PQRS is a rhombus.

